方差齐性检验

来自决策链云智库
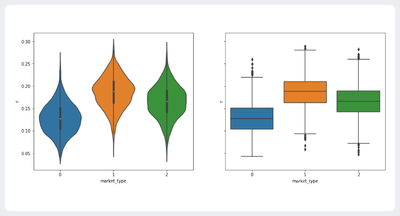
Test for Homogeneity of Variances.png
节点状态
Windows / Windows 10 Win10及以上可用
在V1.0部署
方差齐性检验Test for Homogeneity of Variances.svg
节点开发者决策链算法研发部 (Dev.Team-DPS)
节点英文名Test for Homogeneity of Variances
功能主类别数据分析
英文缩写THomVar
功能亚类别方差分析
节点类型数据挖掘
开发语言R
节点简介

方差齐性检验是一种统计检验方法，用于检验两个或多个样本的方差是否相等。这种检验通常用于分析方差（ANOVA）之前，以确定数据是否满足方差齐性的假设。方差齐性是许多统计方法（如t检验和ANOVA）的一个重要假设。如果数据不满足方差齐性的假设，那么这些方法的结果可能会不准确。因此，在使用这些方法之前，通常需要进行方差齐性检验来确定数据是否满足这一假设。

该模块整合了Levene检验、Bartlett检验和Fligner-Killeen检验三种方法如果方差齐性检验表明数据不满足方差齐性的假设，那么您可以使用一些方法来纠正这一问题。例如，您可以对数据进行变换，或者使用不需要方差齐性假设的非参数方法来分析数据。

用途：用于检验两个或更多的样本组的方差是否相等。如ANOVA（方差分析），需要样本组之间的方差齐性作为预设条件。如果这个条件不满足，那么方差分析的结果可能会出现偏差。

参数：选择分组变量，和连续型数值变量

端口数量与逻辑控制(PC)
Input-入口4个
Output-出口3个
Loop-支持循环是
If/Switch-支持逻辑判断否
输入输出
可生成图片类型（推荐）
可生成数据表类型（推荐）
相关节点
上一节点多重比较方差分析
下一节点Welch检验
WikimediaUI-Globe.svg相关网站




在统计学中，如果一系列随机变量的所有随机变量都具有相同的有限方差，则称为同方差性（模板:IPAc-en），这也被称为方差齐性。相对应的概念被称为异方差性，也称为方差异质性。同k方差性和异k方差性的拼写也经常被使用。[1][2][3] 假设一个变量是同方差性的，而实际上它是异方差性的（模板:IPAc-en），将导致无偏但低效的点估计以及有偏的标准误差估计，并可能导致过高估计拟合优度，如通过皮尔逊系数测量的。

异方差性的存在是回归分析和方差分析中的一个主要关注点，因为它使得假设模型错误都具有相同方差的统计假设检验失效。尽管在异方差性存在的情况下，普通最小二乘估计量仍然是无偏的，但它是低效的，基于同方差性假设的推断是误导的。在那种情况下，过去常常使用广义最小二乘（GLS）。[4][5] 现在，计量经济学中的标准做法是包括异方差性一致标准误差而不是使用GLS，因为如果实际的Skedastic函数未知，GLS在小样本中可能表现出强烈的偏差。[6]

因为异方差性关注错误的第二矩的期望，其存在被称为第二顺序的规范误差。[7]

计量经济学家Robert Engle因其在异方差性存在的情况下对回归分析的研究，并因此提出自回归条件异方差性（ARCH）建模技术，被授予2003年诺贝尔经济学奖。[8]

定义

考虑线性回归方程[math]y_i= x_i \beta_i + \varepsilon_i,\ i = 1,\ldots, N,[/math]，其中依赖随机变量[math]y_i[/math]等于确定性变量[math]x_i[/math]乘以系数[math]\beta_i[/math]加上一个平均值为零的随机干扰项[math]\varepsilon_i[/math]。如果[math]\varepsilon_i[/math]的方差是一个常数[math]\sigma^2[/math]，则干扰项是同方差的；否则，它们是异方差的。特别地，如果[math]\varepsilon_i[/math]的方差依赖于[math]i[/math]或[math]x_i[/math]的值，则干扰项是异方差的。一种可能的异方差性是如果[math]\sigma_i^2= x_i \sigma^2[/math]（一个scedastic函数的例子），因此方差与[math]x[/math]的值成比例。

更一般地，如果干扰项[math]\varepsilon_i[/math]在[math]i[/math]上的方差-协方差矩阵的对角线非常数，则干扰项是异方差的。[9] 下面的矩阵是当只有三个观察值跨越时间时的协方差。矩阵A中的干扰项是同方差的；这是OLS是最佳线性无偏估计器的简单情况。矩阵B和C中的干扰项是异方差的。在矩阵B中，方差随时间变化，随时间稳定增加；在矩阵C中，方差依赖于[math]x[/math]的值。矩阵D中的干扰项是同方差的，因为对角线方差是常数，即使非对角线协方差非零且由于不同的原因普通最小二乘法是低效的：序列相关。

[math]A=\sigma^{2}\left[\begin{array}{lll}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{array}\right] \quad B=\sigma^{2}\left[\begin{array}{lll}1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 3\end{array}\right] \quad C=\sigma^{2}\left[\begin{array}{ccc}x_{1} & 0 & 0 \\ 0 & x_{2} & 0 \\ 0 & 0 & x_{3}\end{array}\right] \quad D=\sigma^{2}\left[\begin{array}{ccc}1 & \rho & \rho^{2} \\ \rho & 1 & \rho \\ \rho^{2} & \rho & 1\end{array}\right][/math]

示例

异方差性通常发生在观察值的大小之间存在较大差异时。

异方差性的一个典型例子是收入与餐饮支出之间的关系。一个富有的人有时可能会吃便宜的食物，而其他时候则吃昂贵的食物。一个贫穷的人几乎总是吃便宜的食物。因此，高收入者在食物支出上显示出更大的变异性。

在一次火箭发射中，观察者每秒测量一次火箭行进的距离。在最初的几秒钟内，测量结果可能精确到最近的厘米。五分钟后，由于距离增加、大气扭曲和其他各种因素，测量的准确性可能仅好到100 m。所以，距离的测量可能表现出异方差性。

后果

经典线性回归模型的一个假设是不存在异方差性。打破这一假设意味着高斯-马尔科夫定理不适用，这意味着OLS估计量不是最佳线性无偏估计器(BLUE)，其方差也不是所有其他无偏估计器中最低的。 异方差性不会导致普通最小二乘法系数估计值有偏，尽管它可以导致普通最小二乘法估计的方差（因此，系数的标准误差）有偏，可能高于或低于真实的人口方差。因此，使用异方差数据进行回归分析仍将提供预测变量和结果之间关系的无偏估计，但标准误差和因此从数据分析获得的推断是可疑的。有偏的标准误差导致有偏的推断，所以假设检验的结果可能是错误的。例如，如果对一个异方差数据集进行OLS，产生有偏的标准误差估计，研究人员可能在给定的显著性水平下未能拒绝原假设，而实际上这个原假设与实际人群的特征不符（犯了第二类错误）。

在某些假设下，即使数据不来自正态分布，OLS估计量在适当的标准化和中心化后也具有正态渐进分布。这一结果用于在进行假设检验时，就算在异方差性下，也使用正态分布或卡方分布（取决于检验统计量的计算方式）。更确切地说，存在异方差性时，OLS估计量在适当的标准化和中心化后是渐进正态的，其方差-协方差矩阵与同方差情况下不同。1980年，White提出了OLS估计量的渐进分布的方差-协方差矩阵的一致估计量。[2]这验证了在异方差性下使用OLS估计量和White的方差-协方差估计量进行假设测试的有效性。

异方差性也是ANOVA问题中遇到的一个主要实际问题。[10] 在某些情况下，F检验仍可使用。[11]

然而，有人说，计量经济学中的学生不应对异方差性反应过度。[3]一位作者写道，“只有当问题严重时，才值得纠正不等误差方差。”[12]此外，另一个警告是，“异方差性从来都不是抛弃一个否则良好的模型的理由。”[3][13]随着异方差性一致标准误差的出现，允许在不指定误差项的条件二阶矩的情况下进行推断，测试条件同方差性不再像过去那样重要。[6]

然而，对于任何非线性模型（例如Logit和Probit模型），异方差性有更严重的后果：参数的最大似然估计（MLE）通常会有偏且不一致（除非似然函数被修改以正确考虑异方差性的确切形式或分布是线性指数族的成员且条件期望函数被正确指定）。[14][15]然而，在二元选择模型（Logit或Probit）的背景下，异方差性只会对错误指定的MLE的渐进均值产生正向缩放效应（即忽略异方差性的模型）。[16]因此，基于错误指定的MLE的预测将保持正确。此外，错误指定的Probit和Logit MLE将是渐进正态分布的，这允许进行通常的显著性测试（使用适当的方差-协方差矩阵）。然而，关于一般假设测试，正如Greene所指出的，“仅仅计算一个鲁棒的协方差矩阵对于一个否则不一致的估计器并不赋予它救赎。因此，在这种设置下鲁棒协方差矩阵的优点是不明确的。”[17]

修正

针对异方差性，存在几种常见的修正方法。它们包括：

  • 数据的稳定化转换，例如对数化数据。未对数化且呈指数增长的序列随着时间的推移往往表现出越来越大的变异性。然而，按百分比计算的变异性可能相对稳定。
  • 使用不同的模型规格（不同的X变量，或者可能是X变量的非线性转换）。
  • 应用加权最小二乘估计方法，在该方法中，将OLS应用于X和Y的转换值或加权值。权重随观察值变化，通常取决于错误方差的变化。在一种变体中，权重直接与因变量的大小相关，这对应于最小二乘百分比回归。[18]
  • 异方差一致标准误差（HCSE），尽管仍有偏差，但改善了OLS估计。[2] HCSE是具有异方差的回归模型中标准误差的一致估计量。该方法在不改变系数值的情况下纠正异方差。如果存在异方差，此方法可能优于常规OLS，因为它可以进行纠正，然而，如果数据是同方差的，标准误差等同于OLS估计的常规标准误差。已经提出了几种改进White方法计算异方差一致标准误差的修正，具有更好的有限样本性质。
  • 野生自助法可以作为一种重采样方法，该方法尊重误差项条件方差的差异。另一种选择是重采样观察值而不是误差。注意，不考虑观察值相关值的重采样误差会强制同方差性，因此产生错误的推断。
  • 使用MINQUE或即使是常用的估计量[math]s_i^2 = (n_i - 1)^{-1} \sum_j \left(y_{ij} - \bar{y}_i\right)^2[/math]（对于[math]i=1,2,...,k[/math]个独立样本，每个样本有[math]j=1, 2, ..., n_i[/math]个观察值），当每个样本的观察值数量较大（[math]n_i > 5[/math]）时，其效率损失不大，尤其是对于小数量的独立样本。[19]

测试

文件:Hsked residual compare.svg
模拟的一阶异方差数据残差的绝对值

可以使用布鲁施-帕根检验来测试残差的同方差性，[20]该检验对独立变量进行残差平方的辅助回归。从这个辅助回归中，保留解释的平方和，除以二，然后成为卡方分布的检验统计量，自由度等于独立变量的数量。[21] 这个卡方检验的零假设是同方差性，备择假设则表明异方差性。由于布鲁施-帕根检验对于正态性的偏离或小样本尺寸敏感，因此通常使用Koenker–Bassett或“广义布鲁施-帕根”检验代替。[22]模板:Additional citation needed 从辅助回归中，保留R平方值，然后乘以样本大小，成为卡方分布的检验统计量（并使用相同的自由度）。尽管对于Koenker–Bassett检验不是必需的，但布鲁施-帕根检验要求将残差平方也除以样本大小除以残差平方和。[22] 可以使用戈尔德菲尔德-昆特检验对组间异方差性进行测试。[23]

由于异方差一致标准误差的标准使用和预检验问题，计量经济学家如今很少使用条件异方差性的检验。[6]

测试列表

尽管可以将组间异方差性的检验正式视为回归模型内部测试的一种特殊情况，但某些检验具有特定于此情况的结构。

模板:Columns-start

回归中的测试

模板:Column

分组数据的测试

模板:Columns-end

广义

同方差分布

两个或更多的正态分布，[math]N(\mu_1,\Sigma_1), N(\mu_2,\Sigma_2), [/math]如果它们在协方差矩阵中共享相同的对角线，[math]\Sigma_1{ii} = \Sigma_2{jj},\ \forall i=j.[/math]且它们的非对角线条目为零，则它们既是同方差的，也缺乏序列相关性。同方差分布在衍生统计模式识别和机器学习算法中特别有用。一个假设同方差性的流行算法示例是费舍尔的线性判别分析。 同方差性的概念可以应用于球面上的分布。[27]

多变量数据

同方差性和异方差性的研究已经推广到了多变量情况，它处理的是向量观测值的协方差而不是标量观测值的方差。其中一个版本是使用协方差矩阵作为多变量离散度的衡量。几位作者在此背景下考虑了测试，包括回归和分组数据情形。[28][29] Bartlett's test用于分组数据之间的异方差性，在单变量情况下最为常见，也已被扩展到多变量情况，但可行的解决方案仅存在于2个组之间。[30] 对于两个以上的组存在近似方法，它们都称为Box's M test。

节点使用的R语言示例代码

方差齐性检验

bartlett.test(x, ...)

leveneTest(y, ...)

fligner.test(x, ...)

方法参见R package: car的官方文档

节点使用指南

  • 用来检验两个或多个独立样本的变量方差是否相等的统计方法
  • 在进行方差分析（ANOVA）或其他需要假设各组方差相等的统计检验前，常常需要先进行方差齐性检验

方法选择

  • Bartlett：对于数据的正态性要求比较高，因为它基于数据分布是正态的假设。最好用于各样本量相等且数据接近正态分布的情况
  • Levene：对数据的正态性要求不如Bartlett检验那么严格，因此相对来说更加稳健。可以用于数据不满足正态分布的情况，比如有偏态或峰态的数据。
  • Fligner-Killeen：一种非参数检验，对数据的分布形态没有特定要求，因此非常稳健。适合用于非正态分布数据或顺序数据的方差齐性检验。

参数配置

  • 统计变量：选择一个或多个连续型数值变量，每个变量与分组变量做一次方差齐性检验
  • 分组变量：选择一个分类分组变量
  • 检验方法：Bartlett，Levene，Fligner-Killeen
  • 筛选阈值：选择需要的P值阈值，节点会自动将满足阈值的变量筛选出，数据集也会同步筛选出满足的变量。
  • 统计变量和分组变量要规避复用
  • 此算法兼容空值

注意事项

  • 不同组别的样本量差异过大可能会影响检验的准确性
  • 当数据违反方差齐性假设时，可以考虑对数据进行转换（如对数转换、平方根转换等）来减少方差不一致的问题

引用

  1. ↑ 关于术语的希腊语词源，请见McCulloch, J. Huston (1985). "On Heteros*edasticity". Econometrica. 53 (2): 483. JSTOR 1911250.
  2. ↑ 2.0 2.1 2.2 2.3 White, Halbert (1980). "A heteroskedasticity-consistent covariance matrix estimator and a direct test for heteroskedasticity". Econometrica. 48 (4): 817–838. CiteSeerX 10.1.1.11.7646. doi:10.2307/1912934. JSTOR 1912934.
  3. ↑ 3.0 3.1 3.2 Gujarati, D. N.; Porter, D. C. (2009). Basic Econometrics (Fifth ed.). Boston: McGraw-Hill Irwin. p. 400. ISBN 9780073375779.
  4. ↑ Goldberger, Arthur S. (1964). Econometric Theory. New York: John Wiley & Sons. pp. 238–243. ISBN 9780471311010.
  5. ↑ Johnston, J. (1972). Econometric Methods. New York: McGraw-Hill. pp. 214–221.
  6. ↑ 6.0 6.1 6.2 Angrist, Joshua D.; Pischke, Jörn-Steffen (2009-12-31). Mostly Harmless Econometrics: An Empiricist's Companion. Princeton University Press. doi:10.1515/9781400829828. ISBN 978-1-4008-2982-8.
  7. ↑ Long, J. Scott; Trivedi, Pravin K. (1993). "Some Specification Tests for the Linear Regression Model". In Bollen, Kenneth A.; Long, J. Scott (eds.). Testing Structural Equation Models. London: Sage. pp. 66–110. ISBN 978-0-8039-4506-7.
  8. ↑ Engle, Robert F. (July 1982). "Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation". Econometrica. 50 (4): 987–1007. doi:10.2307/1912773. ISSN 0012-9682. JSTOR 1912773.
  9. ↑ Peter Kennedy, A Guide to Econometrics, 第五版, p. 137.
  10. ↑ Jinadasa, Gamage; Weerahandi, Sam (1998). "一些在单因素方差分析中的测试的尺寸性能". 统计学通信 - 模拟与计算. 27 (3): 625. doi:10.1080/03610919808813500.
  11. ↑ Bathke, A (2004). "在某些不等方差和非正态数据的平衡设计中，ANOVA F检验仍可使用". 统计计划与推断杂志. 126 (2): 413–422. doi:10.1016/j.jspi.2003.09.010.
  12. ↑ Fox, J. (1997). 应用回归分析、线性模型及相关方法. California: Sage Publications. p. 306.（引用自Gujarati等，2009年，第400页）
  13. ↑ Mankiw, N. G. (1990). "宏观经济学快速复习课程". 经济文献杂志. 28 (4): 1645–1660 [p. 1648]. doi:10.3386/w3256. JSTOR 2727441.
  14. ↑ Giles, Dave (2013年5月8日). "非线性模型的稳健标准误差". 计量经济学拍子. {{cite web}}: Check date values in: |date= (help)
  15. ↑ Gourieroux, C.; Monfort, A.; Trognon, A. (1984). "伪最大似然方法：理论". 计量经济学. 52 (3): 681–700. doi:10.2307/1913471. ISSN 0012-9682.
  16. ↑ Ginker, T.; Lieberman, O. (2017). "对条件异方差性的二元选择模型的鲁棒性". 经济学信函. 150: 130–134. doi:10.1016/j.econlet.2016.11.024.
  17. ↑ Greene, William H. (2012). "二元选择模型中的估计与推断". 计量经济分析 (第七版 ed.). Boston: Pearson Education. pp. 730–755 [p. 733]. ISBN 978-0-273-75356-8.
  18. ↑ Tofallis, C (2008). "Least Squares Percentage Regression". Journal of Modern Applied Statistical Methods. 7: 526–534. doi:10.2139/ssrn.1406472. SSRN 1406472.
  19. ↑ J. N. K. Rao (March 1973). "On the Estimation of Heteroscedastic Variances". Biometrics. 29 (1): 11–24. doi:10.2307/2529672. JSTOR 2529672.
  20. ↑ Breusch, T. S.; Pagan, A. R. (1979). "A Simple Test for Heteroscedasticity and Random Coefficient Variation". Econometrica. 47 (5): 1287–1294. doi:10.2307/1911963. ISSN 0012-9682. JSTOR 1911963.
  21. ↑ Ullah, Muhammad Imdad (2012-07-26). "Breusch Pagan Test for Heteroscedasticity". Basic Statistics and Data Analysis (in English). Retrieved 2020-11-28.
  22. ↑ 22.0 22.1 Pryce, Gwilym. "Heteroscedasticity: Testing and Correcting in SPSS" (PDF). pp. 12–18. Archived (PDF) from the original on 2017-03-27. Retrieved 26 March 2017.
  23. ↑ Baum, Christopher F. (2006). "Stata Tip 38: Testing for Groupwise Heteroskedasticity". The Stata Journal: Promoting Communications on Statistics and Stata (in English). 6 (4): 590–592. doi:10.1177/1536867X0600600412. ISSN 1536-867X. S2CID 117349246.
  24. ↑ R. E. Park (1966). "Estimation with Heteroscedastic Error Terms". Econometrica. 34 (4): 888. doi:10.2307/1910108. JSTOR 1910108.
  25. ↑ Glejser, H. (1969). "A new test for heteroscedasticity". Journal of the American Statistical Association. 64 (325): 316–323. doi:10.1080/01621459.1969.10500976.
  26. ↑ Machado, José A. F.; Silva, J. M. C. Santos (2000). "Glejser's test revisited". Journal of Econometrics. 97 (1): 189–202. doi:10.1016/S0304-4076(00)00016-6.
  27. ↑ Hamsici, Onur C.; Martinez, Aleix M. (2007) [ "Spherical-Homoscedastic Distributions: The Equivalency of Spherical and Normal Distributions in Classification"], Journal of Machine Learning Research, 8, 1583-1623
  28. ↑ Holgersson, H. E. T.; Shukur, G. (2004). "Testing for multivariate heteroscedasticity". Journal of Statistical Computation and Simulation. 74 (12): 879. doi:10.1080/00949650410001646979. hdl:2077/24416. S2CID 121576769.
  29. ↑ Gupta, A. K.; Tang, J. (1984). "Distribution of likelihood ratio statistic for testing equality of covariance matrices of multivariate Gaussian models". Biometrika. 71 (3): 555–559. doi:10.1093/biomet/71.3.555. JSTOR 2336564.
  30. ↑ d'Agostino, R. B.; Russell, H. K. (2005). "Multivariate Bartlett Test". Encyclopedia of Biostatistics. doi:10.1002/0470011815.b2a13048. ISBN 978-0470849071.

查找其他类别的节点，请参考以下列表

取自“https://wiki.statsape.com/index.php?title=方差齐性检验&oldid=9191”