多重比较方差分析

来自决策链云智库
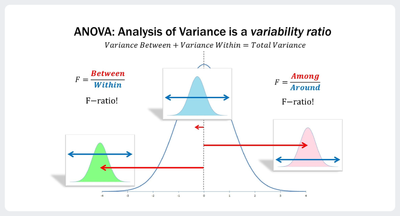
Analysis of Variance Multiple Comparisons.png
节点状态
Windows / Windows 10 Win10及以上可用
在V1.0部署
多重比较方差分析Analysis of Variance Multiple Comparisons.svg
节点开发者决策链算法研发部 (Dev.Team-DPS)
节点英文名Analysis of Variance_Multiple Comparisons
功能主类别数据分析
英文缩写AnaVarMC
功能亚类别方差分析
节点类型数据挖掘
开发语言R
节点简介

方差分析多重比较是在运行完单因素方差分析ANOVA后, 如果该因素影响比较显著，那么需要进一步利用多重比较方法比较该因素不同水平的影响，确定不同水平下该因素的影响是否显著。

用途：用于对ANOVA或其它类型的方差分析后的数据进行深入的分析，检查各组之间的差异。

参数：可以输入多个数值因变量和一个分组变量。可以选择不同检验方法和校正方法。

端口数量与逻辑控制(PC)
Input-入口4个
Output-出口2个
Loop-支持循环是
If/Switch-支持逻辑判断否
输入输出
可生成图片类型（推荐）
可生成数据表类型（推荐）
相关节点
上一节点Two_Way_ANOVA
下一节点方差齐性检验
WikimediaUI-Globe.svg相关网站




在统计学中，多重比较、多重性或多次检验问题出现于当人们同时考虑一组统计推断[1]或者基于观察值估计参数的一个子集[2]时。

随着推断的数量增加，错误推断变得更有可能发生。为了解决这个问题，已经开发了几种统计技术，例如，要求个体比较的严格显著性门槛，以补偿正在进行的推断数量。用于家族误差率控制的方法提供了由于多重比较问题而产生的假阳性率的保证。

历史

多重比较问题在1950年代随着像Tukey和Scheffé这样的统计学家的工作而受到增加的关注。在随后的几十年里，许多程序被开发出来以解决这个问题。1996年，第一次关于多重比较程序的国际会议在特拉维夫举行。[3] 这是一个活跃的研究领域，例如由Emmanuel Candès和Vladimir Vovk.等人进行的工作。

定义

当一个统计分析涉及多个同时进行的统计测试时，就会出现多重比较，每个测试都有可能产生一个“发现”。一个声明的置信水平通常只适用于单独考虑的每个测试，但通常希望对整个同时测试的家族有一个置信水平。[4] 未能补偿多重比较可能会导致重要的现实世界后果，如以下例子所示：

  • 假设治疗是一种教学生写作的新方法，而对照是教学写作的标准方法。可以根据语法、拼写、组织、内容等方面比较两组学生。随着比较的属性越来越多，治疗组和对照组至少在一个属性上看起来不同的可能性就会越来越大，仅仅由于随机抽样误差。
  • 假设我们考虑一种药物在减少任何一个疾病症状方面的有效性。随着考虑的症状越来越多，药物至少在一个症状上看起来比现有药物改善的可能性就会越来越大。

在这两个例子中，随着比较的数量增加，被比较的组在至少一个属性上看起来不同的可能性就会越来越大。如果一个结果是作为涉及多重比较的分析的一部分观察到的，而不是仅涉及单一比较的分析，我们对一个结果将推广到独立数据的信心通常应该更弱。

例如，如果在5%的水平上进行一个测试，并且相应的零假设是真的，错误拒绝零假设的风险只有5%。然而，如果进行100次测试，每次都在5%的水平上，并且所有相应的零假设都是真的，预期数量的错误拒绝（也称为假阳性或类型I错误）是5。如果这些测试在统计上彼此独立（即，是在独立样本上进行的），那么至少有一个错误拒绝的概率大约为99.4%。

多重比较问题也适用于置信区间。一个具有95%覆盖概率水平的单个置信区间将在95%的样本中包含参数的真实值。然而，如果同时考虑100个置信区间，每个都具有95%的覆盖概率，预期的非覆盖区间数量是5。如果区间在统计上彼此独立，那么至少有一个区间不包含总体参数的概率为99.4%。

已经开发了技术来防止由于多个统计测试而发生的假阳性率和非覆盖率的膨胀。

多假设测试的分类

模板:Classification of multiple hypothesis tests

控制程序

WikimediaUI-ArticleDisambiguation-ltr.svg
Further information: Family-wise error rate § Controlling procedures
WikimediaUI-ArticleDisambiguation-ltr.svg
See also: False coverage rate § Controlling procedures, and False discovery rate § Controlling procedures

模板:Image frame

多重检验校正

模板:Cleanup merge 多重检验校正指的是使统计检验更加严格，以对抗多重检验问题。最著名的此类调整是波恩费罗尼校正，但也开发了其他方法。这些方法通常旨在控制家族错误率或假发现率。

如果进行了m次独立比较，则家族错误率（FWER）由下式给出：

[math] \bar{\alpha} = 1-\left( 1-\alpha_{\{\text{per comparison}\}} \right)^m.[/math]

因此，除非测试是完全正相关的（即，相同），否则[math]\bar{\alpha}[/math]会随着比较次数的增加而增加。 如果我们不假设比较是独立的，那么我们仍然可以说：

[math] \bar{\alpha} \le m \cdot \alpha_{\{\text{per comparison}\}},[/math]

这是根据布尔不等式得出的。例如：[math] 0.2649=1-(1-.05)^6 \le .05 \times 6 = 0.3[/math]

有不同的方法可以确保家族错误率最多为[math]\alpha[/math]。最保守的方法，不受依赖和分布假设的限制，是波恩费罗尼校正 [math] \alpha_\mathrm{\{per\ comparison\}}={\alpha}/m[/math]。通过解决[math]m[/math]次独立比较的家族错误率方程得到的略微不那么保守的校正是[math]\alpha_{\{\text{per comparison}\}} = 1-{(1-{\alpha})}^{1/m}[/math]，这被称为Šidák校正。另一种程序是Holm–Bonferroni方法，它通过仅对最低的p值（[math]i=1[/math]）进行最严格的标准测试，以及对更高的p值（[math]i>1[/math]）应用逐渐宽松的标准，从而一致地提供比简单的波恩费罗尼校正更多的功率。[5] [math] \alpha_\mathrm{\{per\ comparison\}}={\alpha}/(m-i+1)[/math]。

对于连续问题，可以采用贝叶斯逻辑根据先验到后验体积比计算[math]m[/math]。波恩费罗尼和Šidák校正的连续泛化在以下文献中提出。[6]

大规模多重检验

传统的多比较校正方法聚焦于为适度数量的比较进行校正，通常用于方差分析。为“大规模多重检验”开发了一套不同的技术，在这种情况下，将进行成千上万次的测试。例如，在基因组学中，使用微阵列等技术时，可以测量数以万计的基因表达水平，以及数百万个遗传标记的基因型。特别是在遗传关联研究领域，非复制性成为了一个严重问题——一个研究中的结果在统计上非常显著，但在后续研究中未能复制。这种非复制性可以有多种原因，但普遍认为未能充分考虑进行多重比较的后果是其中的一个原因。[7] 有人认为，测量和信息技术的进步使得生成大型数据集进行探索性分析变得更加容易，通常导致测试大量假设，而没有先验理由期待许多假设为真。在这种情况下，除非进行多重比较调整，否则预期的假阳性率会非常高。

对于目标是提供明确结果的大规模检测问题，家族错误率仍是赋予统计测试显著性水平的最被接受的参数。另一方面，如果一个研究被视为探索性的，或者显著结果可以在独立的研究中轻松重新测试，控制假发现率（FDR）[8][9][10]经常被偏好。FDR，宽泛定义为所有显著测试中假阳性的预期比例，允许研究人员识别一组“候选阳性”，这些可以在后续研究中进行更严格的评估。[11]

尝试许多未经调整的比较，希望找到一个显著的做法是一个已知问题，无论是无意中还是故意地应用，有时被称为“p-hacking”。[12][13]

评估是否有任何替代假设为真

文件:Quantile meta test.svg
一幅模拟的正态分位数图，用于展示已被标准化为Z分数的一组测试统计量，这些统计量是在零假设下得到的。分布的上尾部偏离沿对角线的预期趋势，是由于存在大量比预期更大的测试统计量值。红色点对应第四大的观测测试统计量，其值为3.13，相比之下预期值为2.06。蓝色点对应第五小的测试统计量，其值为-1.75，相比之下预期值为-1.96。该图表明所有零假设都为真的可能性不大，且大部分或全部真实的替代假设的出现都是由于正向偏差。

在分析一大组测试结果的初始阶段面临的基本问题是，是否有证据表明任何替代假设为真。当假设测试彼此独立时，可以应用的一个简单的元测试是使用Poisson distribution作为模型，来模拟在所有零假设为真时，在给定水平α下会发现的显著结果的数量。, June 2016 {{citation}}: Cite has empty unknown parameters: |cat2=, |cat-date2=, |cat3=, and |cat-date3= (help); Missing or empty |title= (help); Unknown parameter |cat-date= ignored (help); Unknown parameter |cat= ignored (help)[citation needed]如果观察到的正数结果数量明显大于预期，这表明在显著结果中可能存在一些真正的正面结果。

例如，如果进行了1000个独立测试，每个的显著性水平α = 0.05，我们预期当所有零假设为真时会有0.05 × 1000 = 50个显著性测试发生。基于均值为50的泊松分布，观察到超过61个显著性测试的概率小于0.05，因此，如果观察到超过61个显著性结果，很有可能其中一些对应于替代假设成立的情况。这种方法的一个缺点是，当test statistics呈正相关时，它会夸大一些替代假设为真的证据，这在实践中是常见的。, August 2012 {{citation}}: Cite has empty unknown parameters: |cat2=, |cat-date2=, |cat3=, and |cat-date3= (help); Missing or empty |title= (help); Unknown parameter |cat-date= ignored (help); Unknown parameter |cat= ignored (help)[citation needed]另一方面，即使在测试统计量之间存在相关性的情况下，只要泊松分布能够很好地近似显著结果的数量，这种方法仍然有效。这种情况通常出现在从交易数据集中挖掘显著的频繁项集时。此外，一个仔细的两阶段分析可以在预先指定的水平上限定FDR。[14]

另一个常用的方法，适用于可以将test statistics标准化为Z分数的情况，是制作测试统计量的正态分位数图。如果观察到的分位数明显比正态分位数更加分散，这表明一些显著结果可能是真正的正面结果。, January 2012 {{citation}}: Cite has empty unknown parameters: |cat2=, |cat-date2=, |cat3=, and |cat-date3= (help); Missing or empty |title= (help); Unknown parameter |cat-date= ignored (help); Unknown parameter |cat= ignored (help)[citation needed]

节点使用的R语言示例代码

多重比较方差分析

LSD.test(y, trt, DFerror, MSerror, alpha = 0.05, p.adj=c("none","holm","hommel", 
"hochberg", "bonferroni", "BH", "BY", "fdr"), group=TRUE, main = NULL,console=FALSE)

SNK.test(y, trt, DFerror, MSerror, alpha = 0.05, group=TRUE, main = NULL,console=FALSE)

TukeyHSD(x, which, ordered = FALSE, conf.level = 0.95, ...)

dunn_test(data, formula, p.adjust.method = "holm", detailed = FALSE)

方法参见R package: agricolae，rstatix的官方文档

节点使用指南

  • 在ANOVA测试发现至少两组之间存在显著差异之后，进一步确定哪些具体组别之间存在显著差异的方法
  • 在进行多重比较之前，需要首先执行一个普通的ANOVA来确定整体上是否至少有两个组在统计上显著不同
  • 事后测试将提供每对组合比较的P值。根据这些P值，你可以确定哪些组别间存在显著差异

方法选择

  • LSD：当ANOVA显示显著效果，而研究者对第一类错误（假阳性）的控制要求不是很严格时
  • Tukey HSD：当想要对所有可能的组别对进行比较，同时控制整体的第一类错误率
  • SNK：当希望对ANOVA的结果做更细致的分析，但不需要Tukey HSD那么严格的错误率控制
  • Duncan：在初步研究中，希望探索性地发现组间差异，而对第一类错误的控制要求不是非常严格
  • Scheffe：当预期进行大量比较，或者希望进行复杂的比较（如多项式对比）时更为适用
  • Dunn：Dunn测试通常用在非参数统计中，特别是用于Kruskal-Wallis测试后的多重比较，当数据不符合ANOVA的正态分布或方差齐性假设时
  • Nemenyi：在非参数ANOVA之后，当数据分布不满足正态性或方差同质性
  • Conover：适用于数据不满足正态分布或者方差齐性假设的情况，特别是在Friedman检验后进行多重比较时

参数配置

  • 因变量：选择一个或多个连续型数值变量，每个变量和分组变量做一次多重比较方差分析
  • 分组自变量：选择一个分组的变量。如果选择方法是Tukey HSD，分组变量必须是字符串
  • 选择方法：LSD，Tukey HSD，SNK，Duncan，Scheffe，Dunn，Nemenyi，Conover
  • P值校正方法：
    • none：不进行任何校正。每个测试的P值都按原样使用，不考虑多重比较的问题
    • holm：依次将个别P值与根据剩余测试数量调整的显著性水平进行比较，这是Bonferroni方法的改进版
    • hommel：是Holm方法的一种改进，它提供了更强的功效，特别是当一些假设检验的P值非常小的时候
    • hochberg：对Bonferroni方法的又一种改进，它通过按P值的升序对其进行排序，然后依次比较更宽松的调整后的显著性水平，从而提高检验的功效
    • bonferroni：通过将显著性水平除以测试的总数来降低每个测试的显著性标准。这种方法非常保守，可以控制家族错误率（FWER）
    • BH：控制了假发现率（FDR），即被错误地判定为显著的假设检验中的比例。此方法适用于同时控制错误发现和保持检验功效
    • BY：是对BH方法的一种调整，它在任何依赖性结构下都能够控制FDR，但是相比于BH方法更加保守
    • fdr：False Discovery Rate，假发现率校正是一种用于控制多重假设检验中假阳性率的统计方法
  • Nemenyi方法选择：选择Nemenyi方法时，长表输入：需要输入分组，每个变量会做一次检验，通常重复数据。宽表数据：每个变量都代表一个组，不需要分组变量
  • Alpha值：当选择Conover方法时，输入Alpha值，一般输入0.05
  • 因变量和分组自变量要规避复用
  • 此算法兼容空值

注意事项

  • 确保样本是随机的、独立的，并且方差近似相等
  • 样本量对事后测试的统计功效有着重要影响。样本量过小可能导致检测不到实际存在的差异
  • 多重比较增加了第一类错误（假阳性）的风险。因此，事后测试通常会对P值进行校正

引用

  1. ↑ Miller, R.G. (1981). Simultaneous Statistical Inference 2nd Ed. Springer Verlag New York. ISBN 978-0-387-90548-8.
  2. ↑ Benjamini, Y. (2010). "Simultaneous and selective inference: Current successes and future challenges". Biometrical Journal. 52 (6): 708–721. doi:10.1002/bimj.200900299. PMID 21154895. S2CID 8806192.
  3. ↑ "Home". mcp-conference.org.
  4. ↑ Kutner, Michael; Nachtsheim, Christopher; Neter, John; Li, William (2005). Applied Linear Statistical Models. McGraw-Hill Irwin. pp. 744–745. ISBN 9780072386882.
  5. ↑ Aickin, M; Gensler, H (May 1996). "Adjusting for multiple testing when reporting research results: the Bonferroni vs Holm methods". Am J Public Health. 86 (5): 726–728. doi:10.2105/ajph.86.5.726. PMC 1380484. PMID 8629727.
  6. ↑ Bayer, Adrian E.; Seljak, Uroš (2020). "The look-elsewhere effect from a unified Bayesian and frequentist perspective". Journal of Cosmology and Astroparticle Physics. 2020 (10): 009. arXiv:2007.13821. Bibcode:2020JCAP...10..009B. doi:10.1088/1475-7516/2020/10/009. S2CID 220830693.
  7. ↑ Qu, Hui-Qi; Tien, Matthew; Polychronakos, Constantin (2010-10-01). "Statistical significance in genetic association studies". Clinical and Investigative Medicine. 33 (5): E266–E270. ISSN 0147-958X. PMC 3270946. PMID 20926032.
  8. ↑ Benjamini, Yoav; Hochberg, Yosef (1995). "Controlling the false discovery rate: a practical and powerful approach to multiple testing". Journal of the Royal Statistical Society, Series B. 57 (1): 125–133. JSTOR 2346101.
  9. ↑ Storey, JD; Tibshirani, Robert (2003). "Statistical significance for genome-wide studies". PNAS. 100 (16): 9440–9445. Bibcode:2003PNAS..100.9440S. doi:10.1073/pnas.1530509100. JSTOR 3144228. PMC 170937. PMID 12883005.
  10. ↑ Efron, Bradley; Tibshirani, Robert; Storey, John D.; Tusher, Virginia (2001). "Empirical Bayes analysis of a microarray experiment". Journal of the American Statistical Association. 96 (456): 1151–1160. doi:10.1198/016214501753382129. JSTOR 3085878. S2CID 9076863.
  11. ↑ Noble, William S. (2009-12-01). "How does multiple testing correction work?". Nature Biotechnology (in English). 27 (12): 1135–1137. doi:10.1038/nbt1209-1135. ISSN 1087-0156. PMC 2907892. PMID 20010596.
  12. ↑ Young, S. S., Karr, A. (2011). "Deming, data and observational studies" (PDF). Significance. 8 (3): 116–120. doi:10.1111/j.1740-9713.2011.00506.x.{{cite journal}}: CS1 maint: multiple names: authors list (link)
  13. ↑ Smith, G. D., Shah, E. (2002). "Data dredging, bias, or confounding". BMJ. 325 (7378): 1437–1438. doi:10.1136/bmj.325.7378.1437. PMC 1124898. PMID 12493654.{{cite journal}}: CS1 maint: multiple names: authors list (link)
  14. ↑ Kirsch, A; Mitzenmacher, M; Pietracaprina, A; Pucci, G; Upfal, E; Vandin, F (June 2012). "An Efficient Rigorous Approach for Identifying Statistically Significant Frequent Itemsets". Journal of the ACM. 59 (3): 12:1–12:22. arXiv:1002.1104. doi:10.1145/2220357.2220359.

查找其他类别的节点，请参考以下列表

取自“https://wiki.statsape.com/index.php?title=多重比较方差分析&oldid=9203”