回归分析

一组用于估计变量之间关系的统计过程
50个随机点在围绕线性y=1.5x+2（未显示）的高斯分布中的回归线
Part of a series on
Regression analysis
Models
Estimation
Background
Part of a series on
Machine learning
and data mining
Paradigms
Problems
Clustering
Dimensionality reduction
Structured prediction
Anomaly detection
Artificial neural network
Reinforcement learning
Learning with humans
Model diagnostics
Mathematical foundations
Machine-learning venues
Related articles

在统计模型中，回归分析是一组用于估计因变量（通常称为'结果'或'响应'变量，或在机器学习术语中称为'标签'）与一个或多个自变量（通常称为'预测因子'、'协变量'、'解释变量'或'特征'）之间关系的统计过程。回归分析最常见的形式是线性回归，其中找到最符合特定数学标准的数据线（或更复杂的线性组合）。例如，普通最小二乘法计算唯一的线（或超平面），以最小化真实数据与该线（或超平面）之间的平方差之和。出于特定的数学原因（参见线性回归），这允许研究者在自变量取一组特定值时，估计因变量的条件期望（或人口平均值）。较不常见的回归形式使用略有不同的程序来估计其他位置参数（例如，分位数回归或必要条件分析[1]）或在更广泛的非线性模型集合中估计条件期望（例如，非参数回归）。

回归分析主要用于两个概念上不同的目的。首先，回归分析广泛用于预测和预测，在这方面与机器学习领域有着重要的重叠。其次，在某些情况下，回归分析可以用来推断自变量和因变量之间的因果关系。重要的是，回归本身只揭示了在固定数据集中因变量与一系列自变量之间的关系。要分别使用回归进行预测或推断因果关系，研究者必须仔细论证为何现有关系对新情境具有预测力，或为何两变量之间的关系具有因果解释。后者在研究者希望使用观察数据估计因果关系时尤其重要。[2][3]

历史

最早的回归形式是最小二乘法，由勒让德于1805年发表,[4] 以及高斯于1809年发表。[5] 勒让德和高斯都将该方法应用于根据天文观测确定绕太阳运行的天体（主要是彗星，但后来也包括新发现的小行星）的轨道问题。高斯于1821年发表了最小二乘法理论的进一步发展,[6] 包括高斯-马尔可夫定理的一个版本。

“回归”这个术语是由Francis Galton在19世纪创造的，用来描述一个生物现象。这个现象是，高个祖先的后代的身高往往会回归（即regression toward the mean）到一个正常的平均水平。[7][8] 对于Galton而言，回归只有这种生物学意义，[9][10] 但他的工作后来被Udny Yule和Karl Pearson扩展到更一般的统计背景中。[11][12] 在Yule和Pearson的工作中，响应变量和解释变量的joint distribution被假定为高斯分布。这一假设在R.A. Fisher1922年和1925年的作品中被削弱。[13][14][15] Fisher假设响应变量的conditional distribution是高斯的，但联合分布不必是。在这方面，Fisher的假设更接近于高斯在1821年的公式化。

在20世纪50年代和60年代，经济学家使用电动桌面计算器来计算回归。在1970年之前，有时需要长达24小时才能得到一次回归的结果。[16]

回归方法仍然是一个活跃的研究领域。在最近几十年中，已经为robust regression、涉及相关响应的回归（如time series和生长曲线）、预测变量（独立变量）或响应变量是曲线、图像、图表或其他复杂数据对象的回归、适应各种类型缺失数据的回归方法、nonparametric regression、贝叶斯回归方法、预测变量被误差测量的回归、预测变量多于观测的回归，以及与回归的causal inference相关的新方法开发出来。

回归模型

在实践中，研究人员首先选择他们想要估计的模型，然后使用他们选择的方法（例如，ordinary least squares）来估计该模型的参数。回归模型涉及以下几个部分：

  • 未知参数，通常表示为一个标量或向量[math]\beta[/math]。
  • 独立变量，这些在数据中观测到，通常表示为向量[math]X_i[/math]（其中[math]i[/math]表示数据的一行）。
  • 因变量，这些在数据中观测到，通常使用标量[math]Y_i[/math]表示。
  • 误差项，这些在数据中并未直接观测到，通常使用标量[math]e_i[/math]表示。

在各种统计应用领域中，不同的术语被用来代替dependent and independent variables。

大多数回归模型提出：[math]Y_i[/math]是[math]X_i[/math]和[math]\beta[/math]的函数（回归函数），其中[math]e_i[/math]代表一个附加误差项，可能代表[math]Y_i[/math]的未建模决定因素或随机统计噪声：

[math]Y_i = f (X_i, \beta) + e_i[/math]

研究人员的目标是估计与数据最为吻合的函数[math]f(X_i, \beta)[/math]。要进行回归分析，必须指定函数[math]f[/math]的形式。有时这个函数的形式是基于不依赖于数据的[math]Y_i[/math]与[math]X_i[/math]之间关系的知识。如果没有这样的知识，就会选择一个灵活或方便的形式作为[math]f[/math]。例如，一个简单的单变量回归可能提出[math]f(X_i, \beta) = \beta_0 + \beta_1 X_i[/math]，这表明研究者认为[math]Y_i = \beta_0 + \beta_1 X_i + e_i[/math]是对生成数据的统计过程的合理近似。

一旦研究人员确定了他们偏好的统计模型，不同形式的回归分析提供了估计参数[math]\beta[/math]的工具。例如，最小二乘法（包括其最常见的变体，普通最小二乘法）找到使误差平方和[math]\sum_i (Y_i - f(X_i, \beta))^2[/math]最小的[math]\beta[/math]的值。一个给定的回归方法最终会提供[math]\beta[/math]的估计值，通常记为[math]\hat{\beta}[/math]，以区别于生成数据的真实（未知）参数值。使用这个估计值，研究者可以使用拟合值[math]\hat{Y_i} = f(X_i,\hat{\beta})[/math]进行预测或评估模型在解释数据方面的准确性。研究者对估计值[math]\hat{\beta}[/math]或预测值[math]\hat{Y_i}[/math]的兴趣是否内在，取决于上下文和他们的目标。如普通最小二乘法中所述，最小二乘法之所以被广泛使用，是因为估计的函数[math]f(X_i, \hat{\beta})[/math]近似于条件期望[math]E(Y_i|X_i)[/math]。[5]然而，其他变体（例如，最小绝对偏差法或分位数回归法）在研究人员希望建模其他函数[math]f(X_i,\beta)[/math]时是有用的。

需要注意的是，估计回归模型必须有足够的数据。例如，假设一个研究者可以访问[math]N[/math]行数据，包括一个因变量和两个自变量：[math](Y_i, X_{1i}, X_{2i})[/math]。进一步假设研究者希望通过最小二乘法估计一个双变量线性模型：[math]Y_i = \beta_0 + \beta_1 X_{1i} + \beta_2 X_{2i} + e_i[/math]。如果研究者只能访问[math]N=2[/math]个数据点，那么他们可以找到无限多个[math](\hat{\beta}_0, \hat{\beta}_1, \hat{\beta}_2)[/math]的组合，这些组合同样能很好地解释数据：任何满足[math]\hat{Y}_i = \hat{\beta}_0 + \hat{\beta}_1 X_{1i} + \hat{\beta}_2 X_{2i}[/math]的组合，都会导致[math]\sum_i \hat{e}_i^2 = \sum_i (\hat{Y}_i - (\hat{\beta}_0 + \hat{\beta}_1 X_{1i} + \hat{\beta}_2 X_{2i}))^2 = 0[/math]，因此都是合理的解决方案，可以最小化平方残差之和。为了理解为什么有无限多个选项，请注意，[math]N=2[/math]个方程的系统需要为3个未知数求解，这使得系统不确定。或者，人们可以想象无限多个三维平面穿过[math]N=2[/math]个固定点。

更一般地说，要估计一个带有[math]k[/math]个不同参数的最小二乘法模型，必须有[math]N \geq k[/math]个不同的数据点。如果[math]N > k[/math]，那么通常不存在一组参数能完美地拟合数据。数量[math]N-k[/math]在回归分析中经常出现，被称为模型中的自由度。此外，要估计最小二乘法模型，自变量[math](X_{1i}, X_{2i}, ..., X_{ki})[/math]必须是线性独立的：不能通过加和乘以其余自变量来重构任何一个自变量。如普通最小二乘法中所讨论的，这个条件确保了[math]X^{T}X[/math]是一个可逆矩阵，因此存在唯一的解[math]\hat{\beta}[/math]。

潜在假设

本身，回归只是一种使用数据的计算。为了将回归的输出解释为衡量现实世界关系的有意义的统计量，研究人员通常依赖于一些经典的统计假设。这些假设通常包括：

  • 样本代表了整个人群。
  • 自变量测量没有误差。
  • 模型偏差的期望值为零，条件是协变量：[math]E(e_i | X_i) = 0[/math]
  • 残差[math]e_i[/math]的方差在观察中是恒定的（同方差性）。
  • 残差[math]e_i[/math]相互之间是不相关的。从数学上讲，误差的方差-协方差矩阵是对角线的。

为了使最小二乘估计器具有理想的特性，只需满足少数几个条件：特别是，高斯-马尔可夫假设意味着参数估计将是无偏的、一致的，并且在线性无偏估计器类别中是有效的。实践者们开发了多种方法，在现实世界环境中保持这些理想特性的全部或部分，因为这些经典假设不太可能完全成立。例如，对误差-变量进行建模可以得到合理的估计，即使自变量测量时存在误差。异方差一致性标准误差允许[math]e_i[/math]的方差在[math]X_i[/math]的不同值上发生变化。数据子集内存在的或遵循特定模式的相关误差可以使用“群集标准误差、地理加权回归”或纽伊-韦斯特标准误差等技术来处理。当数据行对应于空间中的位置时，如何在地理单元内对[math]e_i[/math]进行建模的选择可能会产生重要后果。[17][18] 计量经济学的子领域主要集中于开发技术，允许研究人员在现实世界设置中得出合理的实际结论，其中经典假设并不完全成立。

线性回归

WikimediaUI-ArticleDisambiguation-ltr.svg
Main article: 线性回归
See 简单线性回归以了解这些公式的推导和一个数值示例

在线性回归中，模型规定是，因变量[math] y_i [/math]是参数的线性组合（但不必是自变量的线性）。例如，在对[math] n [/math]个数据点进行建模的简单线性回归中，有一个自变量：[math] x_i [/math]，和两个参数，[math]\beta_0[/math]和[math]\beta_1[/math]：

直线：[math]y_i=\beta_0 +\beta_1 x_i +\varepsilon_i,\quad i=1,\dots,n.\![/math]

在多元线性回归中，有多个自变量或自变量的函数。

在前面的回归中添加一个[math]x_i^2[/math]项得到：

抛物线：[math]y_i=\beta_0 +\beta_1 x_i +\beta_2 x_i^2+\varepsilon_i,\ i=1,\dots,n.\![/math]

这仍然是线性回归；尽管右侧表达式在自变量[math]x_i[/math]中是二次的，但在参数[math]\beta_0[/math]、[math]\beta_1[/math]和[math]\beta_2[/math]中是线性的。

在这两种情况下，[math]\varepsilon_i[/math]是一个误差项，下标[math]i[/math]索引了特定的观测。

回到直线情况：给定一个来自总体的随机样，我们估计总体参数并获得样本线性回归模型：

[math]\widehat{y}_i = \widehat{\beta}_0 + \widehat{\beta}_1 x_i.[/math]

残差，[math]e_i = y_i - \widehat{y}_i[/math]，是模型预测的因变量值[math]\widehat{y}_i[/math]与因变量真实值[math]y_i[/math]之间的差异。估计的一种方法是普通最小二乘法。该方法获得的参数估计是最小化残差平方和，SSR：

[math]S S R=\sum_{i=1}^{n} e_{i}^{2}[/math]

最小化这个函数得到一组正规方程，这是参数中的一组同时线性方程，通过解这些方程得到参数估计值，[math]\widehat{\beta}_0, \widehat{\beta}_1[/math]。

数据集上线性回归的示意图

在简单回归的情况下，最小二乘估计的公式是

[math]\widehat{\beta}_1=\frac{\sum(x_i-\bar{x})(y_i-\bar{y})}{\sum(x_i-\bar{x})^2}[/math]
[math]\widehat{\beta}_0=\bar{y}-\widehat{\beta}_1\bar{x}[/math]

其中[math]\bar{x}[/math]是[math]x[/math]值的平均值（平均数），[math]\bar{y}[/math]是[math]y[/math]值的平均值。

在假设总体误差项具有恒定方差的情况下，该方差的估计值由下式给出：

[math] \hat{\sigma}^2_\varepsilon = \frac{SSR}{n-2}[/math]

这被称为回归的均方误差（MSE）。分母是样本大小减去从同一数据估计的模型参数数量，[math](n-p)[/math]用于[math]p[/math]个回归量，或者[math](n-p-1)[/math]如果使用了截距。[19] 在这种情况下，[math]p=1[/math]，所以分母是[math]n-2[/math]。

参数估计值的标准误差由下式给出

[math]\hat\sigma_{\beta_1}=\hat\sigma_{\varepsilon} \sqrt{\frac{1}{\sum(x_i-\bar x)^2}}[/math]
[math]\hat\sigma_{\beta_0}=\hat\sigma_\varepsilon \sqrt{\frac{1}{n} + \frac{\bar{x}^2}{\sum(x_i-\bar x)^2}}=\hat\sigma_{\beta_1} \sqrt{\frac{\sum x_i^2}{n}}. [/math]

在进一步假设人口误差项呈正态分布的情况下，研究者可以使用这些估计的标准误差来创建置信区间并进行关于人口参数的假设检验。

广义线性模型

对于衍生方法，参见线性最小二乘法
对于数值示例，参见线性回归

在更一般的多元回归模型中，存在[math]p[/math]个独立变量：

[math] y_i = \beta_1 x_{i1} + \beta_2 x_{i2} + \cdots + \beta_p x_{ip} + \varepsilon_i, \, [/math]

其中[math]x_{ij}[/math]是第[math]i[/math]次观测中的第[math]j[/math]个独立变量。 如果第一个独立变量对于所有的[math]i[/math]都取值为1，即[math]x_{i1} = 1[/math]，那么[math]\beta_1[/math]称为回归截距。

最小二乘参数估计是从[math]p[/math]个正态方程中获得的。残差可以写成

[math]\varepsilon_i=y_i - \hat\beta_1 x_{i1} - \cdots - \hat\beta_p x_{ip}.[/math]

正态方程为

[math]\sum_{i=1}^n \sum_{k=1}^p x_{ij}x_{ik}\hat \beta_k=\sum_{i=1}^n x_{ij}y_i,\ j=1,\dots,p.\,[/math]

在矩阵表示法中，正态方程写为

[math]\mathbf{(X^\top X )\hat{\boldsymbol{\beta}}= {}X^\top Y},\,[/math]

其中[math]\mathbf X[/math]的[math]ij[/math]元素是[math]x_{ij}[/math]，列向量[math]Y[/math]的[math]i[/math]元素是[math]y_i[/math]，[math]j[/math]的[math]\hat{\beta}[/math]元素是[math]\hat{\beta}_{j}[/math]。因此[math]\mathbf X[/math]是[math]n \times p[/math]，[math]Y[/math]是[math]n \times 1[/math]，[math]\hat{\beta}[/math]是[math]p \times 1[/math]。解为

[math]\mathbf{\hat{\boldsymbol{\beta}}= (X^\top X )^{-1}X^\top Y}.[/math]

诊断

WikimediaUI-ArticleDisambiguation-ltr.svg
Main article: 回归诊断
See also: Category:Regression diagnostics

一旦构建了回归模型，确认模型的拟合优度和估计参数的统计显著性可能很重要。常用的拟合优度检验包括决定系数，对残差模式的分析和假设检验。可以通过对整体拟合的F检验，然后是对单个参数的t检验来检查统计显著性。

对这些诊断测试的解释主要依赖于模型的假设。虽然对残差的检查可以用来否定一个模型，但如果违反了模型的假设，t检验或F检验的结果有时难以解释。例如，如果误差项不呈正态分布，在小样本中估计的参数将不会遵循正态分布，从而使推理复杂化。然而，在相对较大的样本中，可以援引中心极限定理，使假设检验可以使用渐近近似进行。

有限依赖变量

有限依赖变量，即只能在一定范围内变化的响应变量，通常出现在计量经济学中。

响应变量可能是非连续的（“限制”在实数线的某个子集上）。对于二元（零或一）变量，如果分析以最小二乘线性回归进行，则该模型被称为线性概率模型。用于二元因变量的非线性模型包括Probit模型和Logit模型。多元Probit模型是估计几个二元因变量与一些自变量之间联合关系的标准方法。对于有两个以上值的分类变量，有多项Logit模型。对于有两个以上值的有序变量，有有序Logit模型和有序Probit模型。当因变量仅有时被观察到时，可以使用截尾回归模型，而当样本不是从感兴趣的人群中随机选择时，可以使用Heckman校正类型的模型。这些程序的替代方法是基于分类变量之间的多元相关性（或多元序列相关性）的线性回归。这些程序在对人群中变量分布的假设上有所不同。如果变量为正值且低值，并且代表某一事件发生的重复，则可以使用像泊松回归或负二项式模型这样的计数模型。

非线性回归

WikimediaUI-ArticleDisambiguation-ltr.svg
Main article: 非线性回归

当模型函数在参数上不是线性的时，必须通过迭代程序最小化平方和。这引入了许多复杂性，这些复杂性在线性和非线性最小二乘法之间的差异中总结。

预测（内插和外推）==

WikimediaUI-ArticleDisambiguation-ltr.svg
Further information: Predicted response and Prediction interval
In the middle, the interpolated straight line represents the best balance between the points above and below this line. The dotted lines represent the two extreme lines. The first curves represent the estimated values. The outer curves represent a prediction for a new measurement.[20]

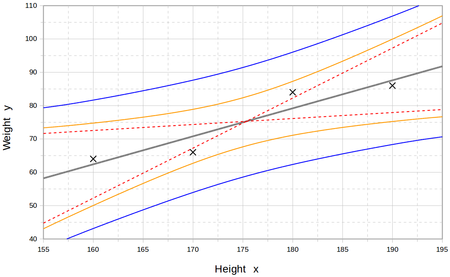
在中间，内插的直线代表了该线上下点的最佳平衡。虚线代表两个极端线。第一个曲线代表估计值。外部曲线代表对新测量的预测。[21]

回归模型预测给定X变量已知值的Y变量值。在用于模型拟合的数据集范围内的预测被非正式地称为内插。超出这一数据范围的预测被称为外推。执行外推强烈依赖于回归假设。外推超出数据的程度越远，模型由于假设与样本数据或真实值之间的差异而失败的空间就越大。

一个预测区间可能伴随着点预测来表示不确定性。这类区间在独立变量的值移动到观测数据所覆盖范围之外时，往往会迅速扩大。

由于这些原因和其他原因，有些人倾向于认为进行外推可能是不明智的。[[22]]

然而，这并不涵盖可能会犯的所有建模错误：特别是假设Y与X之间关系的特定形式。一个恰当进行的回归分析将包括评估所假设形式与观测数据的匹配程度，但它只能在实际可用的独立变量值范围内进行。这意味着任何外推特别依赖于关于回归关系结构形式的假设。如果这种知识包括因变量不能超出某一值域的事实，即使观察到的数据集没有特别靠近此类边界的值，这也可以在选择模型时利用。选择回归的适当功能形式这一步在考虑外推时可能有重大影响。至少，它可以确保由拟合模型产生的任何外推是“现实的”（或与已知情况相符）。

功率和样本量计算

关于观测数与模型中独立变量数之间的关系，目前没有普遍认可的方法。Good和Hardin提出的一种方法是[math]N=m^n[/math]，其中[math]N[/math]是样本量，[math]n[/math]是独立变量的数量，[math]m[/math]是如果模型只有一个独立变量时，达到所需精度所需的观测次数。[23] 例如，一个研究者使用包含1000名病人的数据集建立线性回归模型([math]N[/math])。如果研究者决定需要五次观测来精确定义一条直线([math]m[/math])，那么模型能支持的独立变量的最大数量是4，因为

[math]\frac{\log 1000}{\log5}\approx4.29 [/math]。

其他方法

虽然回归模型的参数通常使用最小二乘法估计，但还使用过其他方法，包括：

软件

For a more comprehensive list, see List of statistical software and 统计软件列表.

所有主要的统计软件包都能进行最小二乘回归分析和推断。简单线性回归和使用最小二乘的多元回归可以在一些电子表格应用程序和部分计算器上完成。虽然许多统计软件包可以执行各种类型的非参数和稳健回归，但这些方法的标准化程度较低。不同的软件包实现不同的方法，且具有特定名称的方法可能在不同的包中有不同的实现。专门的回归软件已为调查分析和神经成像等领域开发。

另行参见

引用

  1. ↑ Necessary Condition Analysis
  2. ↑ David A. Freedman (27 April 2009). Statistical Models: Theory and Practice. Cambridge University Press. ISBN 978-1-139-47731-4.
  3. ↑ R. Dennis Cook; Sanford Weisberg Criticism and Influence Analysis in Regression, Sociological Methodology, Vol. 13. (1982), pp. 313–361
  4. ↑ A.M.勒让德。Nouvelles méthodes pour la détermination des orbites des comètes, Firmin Didot, Paris, 1805。 “Sur la Méthode des moindres quarrés”作为附录出现。
  5. ↑ 5.0 5.1 第1章：Angrist, J. D., & Pischke, J. S. (2008)。 Mostly Harmless Econometrics: An Empiricist's Companion。普林斯顿大学出版社。
  6. ↑ C.F. 高斯。Theoria combinationis observationum erroribus minimis obnoxiae。 (1821/1823)
  7. ↑ Mogull, Robert G. (2004). Second-Semester Applied Statistics. Kendall/Hunt Publishing Company. p. 59. ISBN 978-0-7575-1181-3.
  8. ↑ Galton, Francis (1989). "Kinship and Correlation (reprinted 1989)". Statistical Science. 4 (2): 80–86. doi:10.1214/ss/1177012581. JSTOR 2245330.
  9. ↑ Francis Galton. "Typical laws of heredity", Nature 15 (1877), 492–495, 512–514, 532–533. (Galton uses the term "reversion" in this paper, which discusses the size of peas.)
  10. ↑ Francis Galton. Presidential address, Section H, Anthropology. (1885) (Galton uses the term "regression" in this paper, which discusses the height of humans.)
  11. ↑ Yule, G. Udny (1897). "On the Theory of Correlation". Journal of the Royal Statistical Society. 60 (4): 812–54. doi:10.2307/2979746. JSTOR 2979746.
  12. ↑ Pearson, Karl; Yule, G.U.; Blanchard, Norman; Lee, Alice (1903). "The Law of Ancestral Heredity". Biometrika. 2 (2): 211–236. doi:10.1093/biomet/2.2.211. JSTOR 2331683.
  13. ↑ Fisher, R.A. (1922). "The goodness of fit of regression formulae, and the distribution of regression coefficients". Journal of the Royal Statistical Society. 85 (4): 597–612. doi:10.2307/2341124. JSTOR 2341124. PMC 1084801.
  14. ↑ Ronald A. Fisher (1954). Statistical Methods for Research Workers (Twelfth ed.). Edinburgh: Oliver and Boyd. ISBN 978-0-05-002170-5.
  15. ↑ Aldrich, John (2005). "Fisher and Regression". Statistical Science. 20 (4): 401–417. doi:10.1214/088342305000000331. JSTOR 20061201.
  16. ↑ Rodney Ramcharan. [ Regressions: Why Are Economists Obessessed with Them?] March 2006. Accessed 2011-12-03.
  17. ↑ Fotheringham, A. Stewart; Brunsdon, Chris; Charlton, Martin (2002). 地理加权回归：空间变化关系的分析 (重印 ed.). 英格兰奇切斯特: John Wiley. ISBN 978-0-471-49616-8.
  18. ↑ Fotheringham, AS; Wong, DWS (1991年1月1日). "多元统计分析中的可变区域单元问题". 环境与规划A. 23 (7): 1025–1044. doi:10.1068/a231025. S2CID 153979055. {{cite journal}}: Check date values in: |date= (help)
  19. ↑ Steel, R.G.D, and Torrie, J. H., 统计学原理与程序，特别是生物科学。, 麦格劳-希尔, 1960年，第288页。
  20. ↑ Rouaud, Mathieu (2013). Probability, Statistics and Estimation (PDF). p. 60.
  21. ↑ Rouaud, Mathieu (2013). Probability, Statistics and Estimation. p. 60.
  22. ↑ Chiang, C.L, (2003) Statistical methods of analysis, World Scientific. ISBN 981-238-310-7 - page 274 section 9.7.4 "interpolation vs extrapolation"
  23. ↑ Good, P. I.; Hardin, J. W. (2009). Common Errors in Statistics (And How to Avoid Them) (3rd ed.). Hoboken, New Jersey: Wiley. p. 211. ISBN 978-0-470-45798-6.
  24. ↑ Tofallis, C. (2009). "Least Squares Percentage Regression". Journal of Modern Applied Statistical Methods. 7: 526–534. doi:10.2139/ssrn.1406472. hdl:2299/965. SSRN 1406472.
  25. ↑ YangJing Long (2009). "Human age estimation by metric learning for regression problems" (PDF). Proc. International Conference on Computer Analysis of Images and Patterns: 74–82. {{cite journal}}: |archive-date= requires |archive-url= (help)CS1 maint: url-status (link)

延伸阅读

 :Evan J. Williams, "I. Regression," pp. 523–41.
 :Julian C. Stanley, "II. Analysis of Variance," pp. 541–554.

外部链接

Wikimedia Commons has media related to Regression analysis.
取自“https://wiki.statsape.com/index.php?title=回归分析&oldid=8178”