方差分析(ANOVA)是一系列统计模型及其相关的估计程序(如组间和组内的“变异”)的集合,用于分析均值间的差异。方差分析由统计学家 Ronald Fisher发展而来。方差分析基于总方差定律,即对特定变量中观察到的方差进行分割,将其归因于不同来源的变异组成部分。在最简单的形式中,方差分析提供了一个统计检验,用于判断两个或多个总体平均值是否相等,因此将t-检验推广至超过两个均值的情况。换言之,方差分析用于检验两个或更多均值之间的差异。
历史
根据斯蒂格勒的说法,尽管方差分析在20世纪达到了成熟,但其前身可以追溯到几个世纪之前。[1] 这些包括假设检验、平方和的分割、实验技术和加法模型。拉普拉斯在1770年代就进行了假设检验。[2] 大约在1800年,拉普拉斯和高斯发展了结合观测数据的最小二乘法,该方法改进了当时在天文学和大地测量学中使用的方法。它还启动了对平方和贡献的大量研究。拉普拉斯知道如何从残差(而不是总和)平方和中估计方差。[3] 到1827年,拉普拉斯使用最小二乘法处理关于大气潮汐测量的方差分析问题。[4] 在1800年之前,天文学家已经分离出由反应时间引起的观测误差(所谓的“个人方程”),并开发了减少这些误差的方法。[5] 用于研究个人方程的实验方法后来被新兴的心理学领域接受[6],该领域发展了强大的(全因子)实验方法,并很快加入了随机化和盲化。[7] 在1885年,对加法效应模型的非数学解释非常清晰。[8]
Ronald Fisher于1918年在其关于理论群体遗传学的文章中引入了variance(方差)这一术语,并提出了其正式分析,这篇文章标题为The Correlation Between Relatives on the Supposition of Mendelian Inheritance。[9] 他首次将方差分析应用于数据分析,发表于1921年的作物变异研究I,[10] 该研究将时间序列的变异分成代表年度原因和缓慢恶化的组成部分。Fisher的下一篇文章,与Winifred Mackenzie合著的作物变异研究II,发表于1923年,研究了不同品种和不同肥料处理的地块产量变化。[11] 方差分析在被包含在Fisher 1925年的书籍Statistical Methods for Research Workers后变得广为人知。
随机化模型由多位研究者发展。第一个模型由Jerzy Neyman于1923年用波兰语发表。[12]
示例
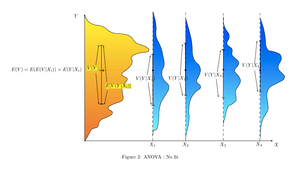
方差分析可以用来描述变量之间的复杂关系。狗展提供了一个例子。狗展并非该品种的随机抽样:它通常限于成年、纯种和典型的狗。展览中狗的体重直方图可能相当复杂,如插图中所示的黄橙色分布。假设我们想要根据每只狗的一组特定特征来预测狗的体重。一种方法是通过根据这些特征将狗群体分成不同组来解释体重分布。一个成功的分组会将狗分成(a)每组狗的体重方差低(意味着该组相对同质)和(b)每组的平均值有所不同(如果两组的平均值相同,则不合理地得出结论认为这些组实际上在任何有意义的方式上是分开的)。
在右侧的插图中,群体被标识为X1、X2等。在第一幅插图中,狗根据两个二元分类的乘积(交互作用)被划分:年轻与老年,短毛与长毛(例如,第1组是年轻的短毛狗,第2组是年轻的长毛狗,等等)。由于每个群体内狗的体重分布(以蓝色显示)具有相对较大的方差,并且由于各组的均值非常相似,因此按这些特征对狗进行分组并不能有效地解释狗体重的变化:知道狗属于哪个组并不能比仅知道狗参加狗展时更好地预测其体重。因此,这种分组未能解释总体分布(黄橙色)中的变化。
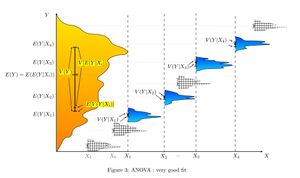
通过将狗分为宠物与工作品种和运动能力较差与较强来尝试解释体重分布可能会更成功(适中匹配)。最重的展览狗很可能是大型、强壮的工作品种,而作为宠物饲养的品种往往体型较小,因此体重较轻。如第二幅插图所示,这些分布的方差明显小于第一种情况,并且均值更加可辨识。然而,分布的显著重叠,例如,意味着我们无法可靠地区分X1和X2。根据硬币翻转来对狗进行分组可能产生看起来相似的分布。
通过品种来解释体重很可能会产生非常好的匹配。所有吉娃娃都很轻,所有圣伯纳德都很重。雪特犬和指示犬之间的体重差异并不足以证明它们是不同的品种。方差分析提供了正式工具来证明这些直观判断。该方法的一个常见用途是分析实验数据或开发模型。该方法相对于相关性有一些优势:并非所有数据都必须是数字,该方法的一个结果是对解释关系的信心的判断。
模型类别
这里概述了用于方差分析的三类模型。
固定效应模型
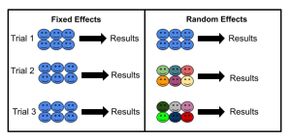
方差分析的固定效应模型(第一类)适用于实验者对实验对象施加一种或多种处理以查看响应变量值是否改变的情况。这使实验者能够估计治疗在整个人群中产生的响应变量值范围。
随机效应模型
当处理不固定时,使用随机效应模型(第二类)。这发生在各种因素水平从较大的人群中抽样时。因为这些水平本身是随机变量,所以一些假设和对比处理的方法(简单差异的多变量概括)与固定效应模型不同。[13]
混合效应模型
混合效应模型(第三类)包含了固定效应和随机效应两种类型的实验因素,这两种类型有着不同的解释和分析方法。
示例
大学或学院部门可以通过教学实验来寻找合适的入门教科书,每本教科书都被视为一种处理方式。固定效应模型将比较候选教科书的列表。随机效应模型将确定在随机选择的教科书列表中是否存在重要差异。混合效应模型将比较现有的(固定的)教科书和随机选择的替代选项。
定义固定效应和随机效应一直是个难题,存在多种竞争性定义。[14]
假设
方差分析已经从几种方法中被研究,其中最常见的是使用一种与处理和区块相关的[线性模型]。请注意,该模型在参数上是线性的,但可能在因素水平上是非线性的。当数据在因素之间平衡时,解释很容易,但对于不平衡的数据则需要更深入的理解。
使用正态分布的教科书分析
方差分析可以用一种[线性模型]来呈现,该模型对响应的[概率分布]做出以下假设:[15][16][17][18]
- [观测独立性]——这是模型的一个假设,简化了统计分析。
- [正态分布]——[残差]的分布是[正态分布]。
- 方差的相等性(或“同方差性”)——即各组数据的方差应该相同。
教科书模型的单独假设意味着对于固定效应模型,[统计错误和残差]是独立的、相同的、并且正态分布的,即错误([math]\varepsilon[/math])是独立且 [math]\varepsilon \thicksim N(0, \sigma^2).[/math]
基于随机化的分析
在[随机对照实验]中,处理方式被随机分配给实验单位,遵循实验协议。这种随机化是客观的,并在实验进行之前声明。客观的随机分配用于测试[零假设]的显著性,遵循[查尔斯·桑德斯·皮尔斯|C. S. Peirce]和[罗纳德·费舍尔]的思想。这种基于设计的分析由[弗朗西斯·J·安斯科姆]在[罗瑟姆斯特德实验站]和[奥斯卡·肯普索恩]在[爱荷华州立大学]讨论和发展。[19] 肯普索恩及其学生假设了“单元处理加性”,这在肯普索恩和[大卫·R·考克斯]的书中进行了讨论。[20][21]
单元-处理加性
在其最简单的形式中,单元-处理加性假设[nb 1]表明,当实验单元[math]i[/math]接受处理[math]j[/math]时观察到的反应[math]y_{i,j}[/math]可以写作该单元的反应[math]y_i[/math]与处理效果[math]t_j[/math]之和,即[22][23][24] [math]y_{i,j}=y_i+t_j.[/math] 单元-处理加性假设意味着,对于每种处理[math]j[/math],第[math]j[/math]种处理对每个实验单元都有完全相同的效果[math]t_j[/math]。
根据Cox和Kempthorne的说法,单元处理加性假设通常不能直接被【可证伪性|证伪】。然而,许多处理单元加性的“后果”是可以被证伪的。对于随机实验,单元-处理加性假设“暗示”所有处理的方差是恒定的。因此,通过【逆否命题】,单元-处理加性的一个必要条件是方差是恒定的。
单元处理加性和随机化的使用与有限群体【调查抽样】中的设计基础推理类似。
衍生的线性模型
Kempthorne利用随机化分布和“单元处理加性”假设产生了一个与教科书模型非常相似的“衍生线性模型”。[25]根据近似定理和模拟研究,这个衍生线性模型的检验统计量可以被适当的正态线性模型的检验统计量紧密近似。[26]但是,存在差异。例如,基于随机化的分析结果显示观测值之间存在微小但(严格)负相关。[27][28]在基于随机化的分析中,没有“正态”分布的假设,当然也没有“独立性”的假设。相反,“观测值是相互依赖的”!
基于随机化的分析的缺点在于,其阐述涉及繁琐的代数和大量的时间。由于基于随机化的分析复杂,并且可以被使用正态线性模型的方法紧密近似,因此大多数教师强调正态线性模型方法。很少有统计学家反对平衡随机实验的模型基础分析。
观测数据的统计模型
然而,当应用于非随机实验或【观察研究|观察性研究】的数据时,基于模型的分析缺乏随机化的保证。
肯普索恩(1979,第125-126页)提到:“实验者必须决定哪些他认为会导致结果变化的原因需要通过实验来控制。那些他没有通过实验控制的原因,因为他没有认识到它们,他必须通过随机化的手段来控制。”他还指出:“只有当实验中的处理由实验者使用完整的随机化程序来应用时,归纳推理的链条才是健全的。只有在这些情况下,实验者才能将他观察到的任何效果仅归因于处理。在这种情况下,他的结论在统计意义上是可靠的。” 对于观测数据,信心区间的推导必须使用“主观”模型,正如罗纳德·费舍尔及其追随者所强调的那样。在实践中,来自观测研究的处理效果估计通常是不一致的。实际上,“统计模型”和观测数据对于提出应该由公众非常谨慎对待的假设是有用的。[29]
假设总结
基于正态模型的方差分析假设残差的独立性、正态性和方差的均匀性。基于随机化的分析只假设残差的方差均匀性(作为单元处理加性的一个后果),并使用实验的随机化程序。这两种分析都需要同方差性,作为正态模型分析的假设,以及作为随机化和加性的后果。
然而,研究改变方差而不是均值的过程(称为离散效应)已成功地使用方差分析进行。[30] 对于方差分析的完整通用性,没有必要的假设,但用于方差分析假设检验的F检验有假设和实际限制,这些仍然是持续关注的对象。
不满足方差分析假设的问题通常可以通过变换来满足假设。
单元处理加性的属性在“变换尺度”下并不是不变的,因此统计学家经常使用变换来实现单元处理加性。如果响应变量预期遵循概率分布的参数族,那么统计学家可能会规定(在实验或观测研究的协议中),响应应进行变换以稳定方差。[31] 此外,如果认为响应遵循乘法模型,统计学家可能会规定对响应进行对数变换。[23][32]
根据柯西的泛函方程定理,对数是唯一将实数乘法变换为加法的连续变换。, 10月 2013 {{citation}}: Cite has empty unknown parameters: |cat2=, |cat-date2=, |cat3=, and |cat-date3= (help); Missing or empty |title= (help); Unknown parameter |cat-date= ignored (help); Unknown parameter |cat= ignored (help)[citation needed]
特征
方差分析(ANOVA)用于比较实验的分析,这些实验中仅对结果的差异感兴趣。实验的统计显著性由两个方差的比率决定。这个比率不受实验观察可能变更的影响:对所有观察值加上一个常数不会改变其显著性;对所有观察值乘以一个常数也不会改变其显著性。因此,ANOVA的统计显著性结果不受常数偏差和缩放误差的影响,也与表达观察值的单位无关。在机械计算时代,通常会从所有观察值中减去一个常数(相当于去除领先数字)以简化数据输入。[33][34] 这是数据编码的一个例子。
算法
ANOVA的计算可以描述为计算多个均值和方差,将两个方差相除,并将比率与手册值进行比较以确定统计显著性。然后,计算处理效果就变得简单了:“任何处理的效果估计是通过取接受处理的观察值的均值与总体均值之间的差值。”[35]
平方和的分割
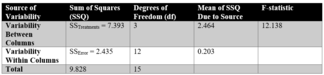
ANOVA使用传统的标准术语。样本方差的定义方程是[math]s^2 = \frac{1}{n-1} \sum_i (y_i-\bar{y})^2[/math],其中除数称为自由度(DF),求和称为平方和(SS),结果称为均方(MS),平方项是与样本均值的偏差。ANOVA估计3个样本方差:基于所有观察值与总体均值偏差的总体方差,基于所有观察值与其相应处理均值偏差的误差方差,以及基于处理均值与总体均值偏差的处理方差。处理方差是基于处理均值与总体均值的偏差计算得出的,结果乘以每种处理中的观察值数量,以解释观察值的方差与均值的方差之间的差异。
基本技术是将总平方和[math]SS[/math]分割成与模型中使用的效应相关的组成部分。例如,一个简化的ANOVA模型,用一种不同水平的处理。
[math]SS_\text{Total} = SS_\text{Error} + SS_\text{Treatments}[/math]
自由度DF的数量可以以类似的方式进行分割:这些组成部分中的一个(用于误差)指定了描述相关平方和的chi-squared distribution,而如果没有处理效应,则对于“处理”也是如此。
[math]DF_\text{Total} = DF_\text{Error} + DF_\text{Treatments}[/math]
F检验
F检验用于比较总偏差的因素。例如,在单因素或单因子ANOVA中,通过比较F检验统计量来检验统计显著性:
[math]F = \frac{\text{处理间方差}}{\text{处理内方差}}[/math] [math]F = \frac{MS_\text{处理}}{MS_\text{误差}} = {{SS_\text{处理} / (I-1)} \over {SS_\text{误差} / (n_T-I)}}[/math]
其中MS是均方,[math]I[/math]是处理的数量,[math]n_T[/math]是案例总数
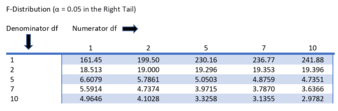
与具有[math]I - 1[/math]为分子自由度和[math]n_T - I[/math]为分母自由度的F分布相比较。使用F分布是一个自然的选择,因为测试统计量是两个按比例求和的平方和的比率,每个都遵循一个按比例的卡方分布。
F的期望值是[math]1 + {n \sigma^2_\text{处理}} / {\sigma^2_\text{误差}}[/math](其中[math]n[/math]是处理样本大小),对于没有处理效果时为1。当F的值超过1时,证据越来越不符合零假设。增加F的两种明显的实验方法是增加样本大小和通过严格的实验控制减少误差方差。
有两种得出ANOVA假设检验结论的方法,两者都产生相同的结果:
- 教科书方法是将观察到的F值与从表中确定的F的临界值进行比较。F的临界值是分子和分母自由度以及显著性水平(α)的函数。如果F ≥ F临界,则拒绝零假设。
- 计算机方法计算F值大于或等于观察值的概率(p-value)。如果这个概率小于或等于显著性水平(α),则拒绝零假设。
ANOVA F检验被认为在最小化假阴性错误的意义上几乎是最优的,对于固定的假阳性错误率(即在固定的显著性水平下最大化功效)。例如,为了检验各种医疗处理具有完全相同效果的假设,F检验的p值与排列检验的p值非常接近:当设计平衡时,这种近似特别接近。[26][36]
诸如permutation test这样的测试被用于表征具有最大功效的测试,以抵御所有替代假设,正如Rosenbaum所观察到的。[nb 2] ANOVA F-检验(关于所有处理效果完全相同的零假设)被推荐为一种实用的测试方法,因为它对许多替代分布具有鲁棒性。[37][nb 3]
扩展算法
ANOVA 包含可分离的部分;方差来源的划分和假设检验可以单独使用。ANOVA 被用来支持其他统计工具。首先使用回归来对数据拟合更复杂的模型,然后使用 ANOVA 来比较模型,目的是选择能够充分描述数据的简单(或更简单)模型。“这些模型可以在不参考 ANOVA 的情况下进行拟合,但随后可以使用 ANOVA 工具来理解拟合模型,并对系数批量的假设进行检验。”[38] “我们认为方差分析是理解和构建多层次模型的一种方式——不是作为回归的替代,而是作为总结复杂的高维推断的工具……”[38]
对单因素的分析
适合进行 ANOVA 分析的最简单实验是具有单一因素的完全随机实验。具有单一因素的更复杂实验涉及随机化的约束,包括完全随机化的区块和拉丁方格(及其变体:希腊-拉丁方格等)。更复杂的实验共享多因素实验的许多复杂性。对完全随机实验的分析(模型、数据汇总、ANOVA 表)有一个相对完整的讨论可以在 这里找到。
有一些替代传统单因素方差分析的方法,例如:Welch's 异方差 F 检验,带修剪均值和温莎化方差的 Welch 异方差 F 检验,Brown-Forsythe 检验,Alexander-Govern 检验,James 二阶检验和 Kruskal-Wallis 检验,可以在 [ onewaytests] R 中找到。
将数据点以以下形式表示是有用的,这种形式被称为统计模型: [math]Y_{ij} = \mu + \tau_j + \varepsilon_{ij}[/math] 其中
- i = 1, 2, 3, ..., R
- j = 1, 2, 3, ..., C
- μ = 总体平均值(均值)
- τj = 与X的j层级相关的差异效应(响应);这假设了总体上τj的值加起来为零(即,[math]\sum_{j = 1}^C \tau_j = 0[/math])
- εij = 与特定的ij数据值相关的噪声或误差
也就是说,我们设想一个加法模型,表示每个数据点可以通过总结三个数量来表示:正在研究的所有因素级别上的真实平均值,加上与特定列(因素级别)相关的增量成分,再加上与影响该特定数据值的所有其他因素相关的最终成分。
对于多个因素
ANOVA概括到研究多个因素的影响。当实验包括每个因素各个水平组合的观测时,称为阶乘实验。阶乘实验比一系列单因素实验更有效,且随着因素数量的增加效率提高。[39] 因此,阶乘设计被广泛使用。
使用ANOVA研究多个因素的影响有一个复杂性。在具有因素x、y和z的3因素ANOVA中,ANOVA模型包括主效应(x、y、z)的项和交互作用(xy、xz、yz、xyz)的项。
所有项都需要假设检验。交互作用项的增加增加了某些假设检验偶然产生假阳性的风险。幸运的是,经验表明高阶交互作用很少见。[40] , 12月 2014 {{citation}}: Cite has empty unknown parameters: |cat2=, |cat-date2=, |cat3=, and |cat-date3= (help); Missing or empty |title= (help); Unknown parameter |cat-date= ignored (help); Unknown parameter |cat= ignored (help)[verification needed]
检测交互作用的能力是多因素ANOVA的一个主要优势。一次测试一个因素会隐藏交互作用,但会产生看似不一致的实验结果。[39]
遇到交互作用时应谨慎;首先测试交互作用项,如果发现交互作用,应扩展分析范围超出ANOVA。关于在遇到交互作用后继续进行ANOVA程序的建议,文献中的观点各不相同。交互作用使实验数据的解释复杂化。既不能简单地接受显著性计算,也不能直接采纳估计的处理效应。"一个显著的交互作用通常会掩盖主效应的显著性。"[41] 推荐使用图形方法来增强理解。回归分析通常很有用。Cox (1958)提供了关于交互作用的详尽讨论。[42] 一些交互作用可以通过变换来消除,而另一些则不能。
多因素ANOVA采用多种技术以降低成本。其中一种技术用于阶乘设计,旨在最小化重复(可能在支持分析技巧的情况下不进行重复)并在发现效果在统计上(或实际上)不显著时合并群组。拥有许多不显著因素的实验可能会塌陷为一个由许多重复支持的少数因素的实验。[43]
相关分析
一些分析是为了支持实验的设计而必需的,而其他分析则在正式发现因素变化导致响应中的统计显著变化后进行。由于实验是迭代的,一个实验的结果会改变后续实验的计划。
准备分析
实验单位的数量
在设计实验时,计划实验单位的数量是为了满足实验的目标。实验通常是顺序进行的。
早期实验通常旨在提供无偏差的处理效果和实验误差的均值估计。后期实验通常设计用于测试假设,即某个处理效果具有重要的量级;在这种情况下,选择实验单位的数量是为了确保实验预算内可行并具有足够的力量,以及满足其他目标。
在心理学中通常要求报告样本大小分析。"提供样本大小信息以及导致样本大小决策的过程。"[44] 这种分析在实验进行前的实验协议中写明,并在赠款申请和行政审查委员会中进行审查。
除了功效分析,还有一些非正式的方法用于选择实验单位的数量。这些包括基于限制假阴性错误概率的图形方法、基于预期变异增加(超过残差)的图形方法以及基于实现所需置信区间的方法。[45]
功效分析
功效分析经常在ANOVA的背景下应用,以评估如果我们假设某种ANOVA设计、群体中的效果大小、样本大小和显著性水平,则成功拒绝零假设的概率。功效分析可以通过确定为了有合理机会在备择假设为真时拒绝零假设而需要的样本大小来协助研究设计。[46][47][48][49]
效果大小
为ANOVA提出了几种标准化的效果量度,以总结预测变量与因变量之间的关联强度或完整模型的整体标准化差异。标准化效果大小估计促进了跨研究和学科的发现比较。然而,虽然标准化效果大小在许多专业文献中常用,但立即具有“有意义”单位的非标准化效果大小度量可能更适合报告目的。[50]
模型确认
有时会进行测试以确定是否违反了ANOVA的假设。残差被检查或分析以确认homoscedasticity和总体正态性。[51] 残差在作为任何事物(包括时间和模型化数据值)的函数绘制时,应呈现出(零均值正态分布)噪声的外观。趋势暗示了因素之间或观察之间的相互作用。
后续测试
在ANOVA中,一个统计上显著的效果通常会进行额外的测试。这样做是为了评估哪些组与哪些其他组不同,或测试各种其他专注的假设。后续测试通常根据它们是“计划内的”(a priori)还是"事后"区分开。计划内的测试是在查看数据之前确定的,而事后测试则是在查看数据之后才构思的(尽管“事后”这个术语的使用并不一致)。
后续测试可能是对单个组平均值的“简单”成对比较,或可能是“复合”比较(例如,比较组A、B和C的平均值与组D的平均值)。比较还可以查看趋势测试,例如当自变量涉及有序级别时的线性和二次关系。后续测试通常包含调整multiple comparisons problem的方法。
用于识别哪些特定组、变量或因素的平均值统计上不同的后续测试包括Tukey's range test和Duncan's new multiple range test。反过来,这些测试经常会使用Compact Letter Display (CLD)方法来进行,以使得提到的测试的输出对非统计学者的观众更加透明。
研究设计
有几种类型的ANOVA。许多统计学家将ANOVA基于实验设计,[52] 特别是基于指定将处理随机分配给对象的协议;协议对分配机制的描述应包括对处理的结构和任何阻塞的规定。将ANOVA应用于使用适当的统计模型的观察数据也很常见。[53]
一些流行的设计使用以下类型的方差分析(ANOVA):
- 单因素方差分析(One-way ANOVA)用于检验两个或多个independent组(均值)之间的差异,例如,作物施用尿素的不同水平,或几种不同细菌物种对抗生素作用的不同水平,[54] 或某些药物对患者组的不同影响水平。然而,如果这些组不是独立的,并且组之间有顺序(如轻、中、重症),或者给同一组患者的药物剂量(如5mg/mL、10mg/mL、20mg/mL),则应使用linear trend estimation。通常情况下,单因素方差分析用于测试至少三个组之间的差异,因为两组案例可以由t-test涵盖。[55] 当只有两个均值需要比较时,t-test和ANOVA的F-test是等效的;ANOVA和t之间的关系由[math]1=F = t^2[/math]给出。
- 因子实验(Factorial)方差分析用于有多个因素时。
- 重复测量方差分析(Repeated measures ANOVA)用于每个因素都使用相同受试者的情况(例如,在longitudinal study中)。
- 多变量方差分析(MANOVA)用于有多个response variable的情况。
注意事项
平衡实验(每种处理的样本量相等)相对容易解释;不平衡实验提供了更多的复杂性。对于单因素(单向)ANOVA,不平衡数据的调整很容易,但不平衡分析缺乏稳健性和力量。[56] 对于更复杂的设计,缺乏平衡导致了进一步的复杂性。"平衡数据中主效应和交互作用的正交性质不会延续到不平衡情况。这意味着通常的方差分析技术不适用。因此,不平衡因子的分析比平衡设计的分析要困难得多。"[57] 在一般情况下,“方差分析也可以应用于不平衡数据,但这样的话,平方和、均方和‘'F'’比将取决于考虑变异来源的顺序。”[38]
方差分析(ANOVA)部分是一个统计显著性检验。美国心理学会(以及许多其他组织)认为,仅报告统计显著性是不够的,更倾向于报告置信区间。[50]
概括
方差分析被认为是linear regression的一个特例[58][59],而线性回归又是general linear model的一个特例。[60] 所有这些都认为观测值是模型(拟合)和需要最小化的残差(误差)之和。
Kruskal-Wallis检验和Friedman检验是不依赖于正态分布假设的非参数检验。[61][62]
与线性回归的联系
下面我们阐明多因素方差分析(ANOVA)与线性回归之间的联系。
将数据线性重排,使得第[math]k[/math]个观测值与一个响应[math]y_k[/math]和因子[math]Z_{k,b}[/math]相关联,其中[math] \in \{1,2,\ldots,B\}[/math]表示不同的因子,[math]B[/math]是因子的总数。在单因素ANOVA中,[math]B=1[/math];在双因素ANOVA中,[math]B = 2[/math]。此外,我们假设第[math]b[/math]个因子有[math]I_b[/math]个水平,即[math]\{1,2,\ldots,I_b\}[/math]。现在,我们可以将因子通过one-hot编码为[math]\sum_{b=1}^B I_b[/math]维向量[math]v_k[/math]。
one-hot编码函数[math]g_b : \{1,2,\ldots,I_b\} \mapsto \{0,1\}^{I_b}[/math]的定义是,[math]g_b(Z_{k,b})[/math]的第[math]i[/math]个元素为 [math]g_b(Z_{k,b})_i = \begin{cases} 1 & \text{如果 } i=Z_{k,b} \\ 0 & \text{其他情况} \end{cases}[/math] 向量[math]v_k[/math]是所有上述向量的连接,对所有的[math]b[/math]而言。因此,[math]v_k = [g_1(Z_{k,1}), g_2(Z_{k,2}), \ldots, g_B(Z_{k,B})][/math]。为了获得一个完全通用的[math]B[/math]因素交互作用ANOVA,我们必须在向量[math]v_k[/math]中连接每一个额外的交互项,然后添加一个截距项。让这个向量为[math]X_k[/math]。
有了这个符号,我们现在就有了与线性回归的确切联系。我们只需将响应[math]y_k[/math]对向量[math]X_k[/math]进行回归。然而,存在关于可识别性的担忧。为了克服这些问题,我们假设每组交互作用内的参数之和等于零。从这里,可以使用F统计量或其他方法来确定个别因素的相关性。
示例
我们可以考虑一个2因素交互作用的例子,假设第一个因素有2个水平,第二个因素有3个水平。
定义[math]a_i = 1[/math],如果[math]Z_{k,1}=i[/math];[math]b_i = 1[/math],如果[math]Z_{k,2} = i[/math]。即,[math]a[/math]是第一个因素的one-hot编码,[math]b[/math]是第二个因素的one-hot编码。
据此, [math] X_k = [a_1, a_2, b_1, b_2, b_3 ,a_1 \times b_1, a_1 \times b_2, a_1 \times b_3, a_2 \times b_1, a_2 \times b_2, a_2 \times b_3, 1] [/math] 其中最后一项是截距项。更具体的例子假设 [math]\begin{align} Z_{k,1} & = 2 \\ Z_{k,2} & = 1 \end{align}[/math] 那么,[math]X_k = [0,1,1,0,0,0,0,0,1,0,0,1][/math]
另行参见
- ANOVA on ranks
- ANOVA-simultaneous component analysis
- Analysis of covariance (ANCOVA)
- Analysis of molecular variance (AMOVA)
- Analysis of rhythmic variance (ANORVA)
- Expected mean squares
- Explained variation
- Linear trend estimation
- Mixed-design analysis of variance
- Multivariate analysis of covariance (MANCOVA)
- Permutational analysis of variance
- Variance decomposition
脚注
- ↑ 在大多数文本中,单元-处理加性简称为加性。Hinkelmann和Kempthorne添加形容词,并区分严格和广义上的加性。这允许详细考虑多个错误来源(处理、状态、选择、测量和抽样),见第161页。
- ↑ Rosenbaum (2002, page 40) 引用了 Section 5.7 (Permutation Tests),Theorem 2.3 (实际上是 Theorem 3, page 184) 来自Lehmann的《Testing Statistical Hypotheses》(1959)。
- ↑ 用于比较方差的F-检验声誉好坏参半。它不被推荐作为假设检验来确定两个不同样本是否具有相同的方差。但它被推荐用于ANOVA,其中比较的是同一个样本的两个方差估计。虽然F-检验通常对于正态分布的偏离并不鲁棒,但在ANOVA的特殊情况下,它被发现是鲁棒的。来自 Moore & McCabe (2003) 的引用:“方差分析使用 F 统计量,但这些并不同于用于比较两个群体标准差的 F 统计量。”(第554页)“关于方差的 F 检验和其他推断程序缺乏鲁棒性,以至于在实践中几乎没什么用。”(第556页)“[ANOVA F-检验]对于适度的非正态性和不等方差相对不敏感,特别是当样本量相似时。”(第763页)ANOVA 假设同方差性,但它是鲁棒的。同方差性的统计检验(F-检验)不是鲁棒的。Moore & McCabe 推荐一个经验法则。
引用笔记
- ↑ Stigler (1986)
- ↑ Stigler (1986, p 134)
- ↑ Stigler (1986, p 153)
- ↑ Stigler (1986, pp 154–155)
- ↑ Stigler (1986, pp 240–242)
- ↑ Stigler (1986, 第7章 – 心理物理学作为对比点)
- ↑ Stigler (1986, p 253)
- ↑ Stigler (1986, pp 314–315)
- ↑ The Correlation Between Relatives on the Supposition of Mendelian Inheritance. Ronald A. Fisher. Philosophical Transactions of the Royal Society of Edinburgh. 1918. (第52卷, 页码 399–433)
- ↑ Fisher, Ronald A. (1921). ") 作物变异研究I. Broadbalk精选谷物产量的检验". 农业科学杂志. 11 (2): 107–135. doi:10.1017/S0021859600003750. hdl:2440/15170. S2CID 86029217.
- ↑ Fisher, Ronald A. (1923). ") 作物变异研究II. 不同马铃薯品种的施肥反应". 农业科学杂志. 13 (3): 311–320. doi:10.1017/S0021859600003592. hdl:2440/15179. S2CID 85985907.
- ↑ Scheffé (1959, 第291页, "随机化模型最初由Neyman (1923)为完全随机设计所制定,由Neyman (1935)为随机区块设计,由Welch (1937)和Pitman (1937)为某一特定零假设下的拉丁方设计,以及由Kempthorne (1952, 1955)和Wilk (1955)为许多其他设计。")
- ↑ Montgomery (2001, 第12章:带有随机因子的实验)
- ↑ Gelman (2005, pp. 20–21)
- ↑ Snedecor, George W.; Cochran, William G. (1967). Statistical Methods (6th ed.). p. 321.
- ↑ Cochran & Cox (1992, p 48)
- ↑ Howell (2002, p 323)
- ↑ Anderson, David R.; Sweeney, Dennis J.; Williams, Thomas A. (1996). Statistics for business and economics (6th ed.). Minneapolis/St. Paul: West Pub. Co. pp. 452–453. ISBN 978-0-314-06378-6.
- ↑ Anscombe (1948)
- ↑ Hinkelmann, Klaus; Kempthorne, Oscar (2005). Design and Analysis of Experiments, Volume 2: Advanced Experimental Design (in English). John Wiley. p. 213. ISBN 978-0-471-70993-0.
- ↑ Cox, D. R. (1992). Planning of Experiments (in English). Wiley. ISBN 978-0-471-57429-3.
- ↑ Kempthorne (1979, p 30)
- ↑ 23.0 23.1 Cox (1958, 第2章:一些关键假设)
- ↑ Hinkelmann和Kempthorne (2008, 第1卷,贯穿全文。在第2.3.3节介绍:实验设计原则;线性模型;模型概述)
- ↑ Hinkelmann和Kempthorne (2008, 第1卷,第6.3节:完全随机设计;衍生线性模型)
- ↑ 26.0 26.1 Hinkelmann和Kempthorne (2008, 第1卷,第6.6节:完全随机设计;近似随机化测试)
- ↑ Bailey (2008, 第2.14章 "更一般的模型" in Bailey, pp. 38–40)
- ↑ Hinkelmann和Kempthorne (2008, 第1卷,第7章:处理比较)
- ↑ Freedman , 11月 2012
{{citation}}: Cite has empty unknown parameters:|cat2=,|cat-date2=,|cat3=, and|cat-date3=(help); Missing or empty|title=(help); Unknown parameter|cat-date=ignored (help); Unknown parameter|cat=ignored (help)[full citation needed] - ↑ Montgomery (2001, 第3.8节:发现离散效应)
- ↑ Hinkelmann 和 Kempthorne (2008, 第1卷,第6.10节:完全随机设计;变换)
- ↑ Bailey (2008)
- ↑ Montgomery (2001, 第3-3节:单因素实验:方差分析;固定效应模型分析)
- ↑ Cochran & Cox (1992, 第2页示例)
- ↑ Cochran & Cox (1992, 第49页)
- ↑ Hinkelmann and Kempthorne (2008, Volume 1, Section 6.7: 完全随机设计;CRD具有不等数量的重复)
- ↑ Moore and McCabe (2003, page 763)
- ↑ 38.0 38.1 38.2 Gelman (2008)
- ↑ 39.0 39.1 Montgomery (2001, 第5-2节:阶乘设计简介;阶乘的优点)
- ↑ Belle (2008, 第8.4节:高阶交互作用很少发生)
- ↑ Montgomery (2001, 第5-1节:阶乘设计简介;基本定义和原则)
- ↑ Cox (1958, 第6章:关于阶乘实验的基本思想)
- ↑ Montgomery (2001, Section 5-3.7: Introduction to factorial designs; The two-factor factorial design; One observation per cell)
- ↑ Wilkinson (1999, p 596)
- ↑ Montgomery (2001, Section 3-7: Determining sample size)
- ↑ Howell (2002, Chapter 8: Power)
- ↑ Howell (2002, Section 11.12: Power (in ANOVA))
- ↑ Howell (2002, Section 13.7: Power analysis for factorial experiments)
- ↑ Moore and McCabe (2003, pp 778–780)
- ↑ 50.0 50.1 Wilkinson (1999, p 599)
- ↑ Montgomery (2001, Section 3-4: Model adequacy checking)
- ↑ Cochran & Cox (1957, p 9, "The general rule [is] that the way in which the experiment is conducted determines not only whether inferences can be made, but also the calculations required to make them.")
- ↑ "ANOVA Design". bluebox.creighton.edu. Retrieved 23 1月 2023.
- ↑ "One-way/single factor ANOVA". Archived from the original on 7 11月 2014.
{{cite web}}:|archive-date=/|archive-url=timestamp mismatch; 7 11月 2014 suggested (help) - ↑ "The Probable Error of a Mean". Biometrika. 6: 1–25. 1908. doi:10.1093/biomet/6.1.1. hdl:10338.dmlcz/143545.
- ↑ Montgomery (2001, Section 3-3.4: Unbalanced data)
- ↑ Montgomery (2001, Section 14-2: Unbalanced data in factorial design)
- ↑ Gelman (2005, p.1) (with qualification in the later text)
- ↑ Montgomery (2001, Section 3.9: The Regression Approach to the Analysis of Variance)
- ↑ Howell (2002, p 604)
- ↑ Howell (2002, Chapter 18: Resampling and nonparametric approaches to data)
- ↑ Montgomery (2001, Section 3-10: Nonparametric methods in the analysis of variance)
其他引用
- Anscombe, F. J. (1948). "The Validity of Comparative Experiments". Journal of the Royal Statistical Society. Series A (General). 111 (3): 181–211. doi:10.2307/2984159. JSTOR 2984159. MR 0030181.
- Bailey, R. A. (2008). Design of Comparative Experiments. Cambridge University Press. ISBN 978-0-521-68357-9. Pre-publication chapters are available on-line.
- Belle, Gerald van (2008). Statistical rules of thumb (2nd ed.). Hoboken, N.J: Wiley. ISBN 978-0-470-14448-0.
- Cochran, William G.; Cox, Gertrude M. (1992). Experimental designs (2nd ed.). New York: Wiley. ISBN 978-0-471-54567-5.
- Cohen, Jacob (1988). Statistical power analysis for the behavior sciences (2nd ed.). Routledge ISBN 978-0-8058-0283-2
- Cohen, Jacob (1992). "Statistics a power primer". Psychological Bulletin. 112 (1): 155–159. doi:10.1037/0033-2909.112.1.155. PMID 19565683. S2CID 14411587.
- Cox, David R. (1958). Planning of experiments. Reprinted as ISBN 978-0-471-57429-3
- Cox, David R. (2006). Principles of statistical inference. Cambridge New York: Cambridge University Press. ISBN 978-0-521-68567-2.
- Freedman, David A.(2005). Statistical Models: Theory and Practice, Cambridge University Press. ISBN 978-0-521-67105-7
- Gelman, Andrew (2005). "Analysis of variance? Why it is more important than ever". The Annals of Statistics. 33: 1–53. arXiv:math/0504499. doi:10.1214/009053604000001048. S2CID 13529149.
- Gelman, Andrew (2008). "Variance, analysis of". The new Palgrave dictionary of economics (2nd ed.). Basingstoke, Hampshire New York: Palgrave Macmillan. ISBN 978-0-333-78676-5.
- Hinkelmann, Klaus & Kempthorne, Oscar (2008). Design and Analysis of Experiments. Vol. I and II (Second ed.). Wiley. ISBN 978-0-470-38551-7.
- Howell, David C. (2002). Statistical methods for psychology (5th ed.). Pacific Grove, CA: Duxbury/Thomson Learning. ISBN 978-0-534-37770-0.
- Kempthorne, Oscar (1979). The Design and Analysis of Experiments (Corrected reprint of (1952) Wiley ed.). Robert E. Krieger. ISBN 978-0-88275-105-4.
- Lehmann, E.L. (1959) Testing Statistical Hypotheses. John Wiley & Sons.
- Montgomery, Douglas C. (2001). Design and Analysis of Experiments (5th ed.). New York: Wiley. ISBN 978-0-471-31649-7.
- Moore, David S. & McCabe, George P. (2003). Introduction to the Practice of Statistics (4e). W H Freeman & Co. ISBN 0-7167-9657-0
- Rosenbaum, Paul R. (2002). Observational Studies (2nd ed.). New York: Springer-Verlag. ISBN 978-0-387-98967-9
- Scheffé, Henry (1959). The Analysis of Variance. New York: Wiley.
- Stigler, Stephen M. (1986). The history of statistics : the measurement of uncertainty before 1900. Cambridge, Mass: Belknap Press of Harvard University Press. ISBN 978-0-674-40340-6.
- Wilkinson, Leland (1999). "Statistical Methods in Psychology Journals; Guidelines and Explanations". American Psychologist. 5 (8): 594–604. CiteSeerX 10.1.1.120.4818. doi:10.1037/0003-066X.54.8.594. S2CID 428023.
延伸阅读
This 'further reading' section may need cleanup. (November 2014) |
- Box, G. e. p. (1953). "Non-Normality and Tests on Variances". Biometrika. 40 (3/4): 318–335. doi:10.1093/biomet/40.3-4.318. JSTOR 2333350.
- Box, G. E. P. (1954). "Some Theorems on Quadratic Forms Applied in the Study of Analysis of Variance Problems, I. Effect of Inequality of Variance in the One-Way Classification". The Annals of Mathematical Statistics. 25 (2): 290. doi:10.1214/aoms/1177728786.
- Box, G. E. P. (1954). "Some Theorems on Quadratic Forms Applied in the Study of Analysis of Variance Problems, II. Effects of Inequality of Variance and of Correlation Between Errors in the Two-Way Classification". The Annals of Mathematical Statistics. 25 (3): 484. doi:10.1214/aoms/1177728717.
- Caliński, Tadeusz; Kageyama, Sanpei (2000). Block designs: A Randomization approach, Volume I: Analysis. Lecture Notes in Statistics. Vol. 150. New York: Springer-Verlag. ISBN 978-0-387-98578-7.
- Christensen, Ronald (2002). Plane Answers to Complex Questions: The Theory of Linear Models (Third ed.). New York: Springer. ISBN 978-0-387-95361-8.
- Cox, David R. & Reid, Nancy M. (2000). The theory of design of experiments. (Chapman & Hall/CRC). ISBN 978-1-58488-195-7
- Fisher, Ronald (1918). "Studies in Crop Variation. I. An examination of the yield of dressed grain from Broadbalk" (PDF). Journal of Agricultural Science. 11 (2): 107–135. doi:10.1017/S0021859600003750. hdl:2440/15170. S2CID 86029217. Archived from the original (PDF) on 12 6月 2001.
{{cite journal}}:|archive-date=/|archive-url=timestamp mismatch; 12 6月 2001 suggested (help) - Freedman, David A.; Pisani, Robert; Purves, Roger (2007) Statistics, 4th edition. W.W. Norton & Company ISBN 978-0-393-92972-0
- Hettmansperger, T. P.; McKean, J. W. (1998). Edward Arnold (ed.). Robust nonparametric statistical methods. Kendall's Library of Statistics. Vol. 5 (First ed.). New York: John Wiley & Sons, Inc. pp. xiv+467 pp. ISBN 978-0-340-54937-7. MR 1604954.
- Lentner, Marvin; Thomas Bishop (1993). Experimental design and analysis (Second ed.). Blacksburg, VA: Valley Book Company. ISBN 978-0-9616255-2-8.
- Tabachnick, Barbara G. & Fidell, Linda S. (2007). Using Multivariate Statistics (5th ed.). Boston: Pearson International Edition. ISBN 978-0-205-45938-4
- Wichura, Michael J. (2006). The coordinate-free approach to linear models. Cambridge Series in Statistical and Probabilistic Mathematics. Cambridge: Cambridge University Press. pp. xiv+199. ISBN 978-0-521-86842-6. MR 2283455.
- Phadke, Madhav S. (1989). Quality Engineering using Robust Design. New Jersey: Prentice Hall PTR. ISBN 978-0-13-745167-8.
外部链接
- SOCR: ANOVA Activity
- Examples of all ANOVA and ANCOVA models with up to three treatment factors, including randomized block, split plot, repeated measures, and Latin squares, and their analysis in R (University of Southampton)
- NIST/SEMATECH e-Handbook of Statistical Methods, section 7.4.3: "Are the means equal?"
- Analysis of variance: Introduction