分位回归：修订间差异

来自决策链云智库
无编辑摘要
无编辑摘要
第2行： 第2行：
|nodename=分位回归
|nodename=分位回归
|nodeimage=Quantile Regression.png
|nodeimage=Quantile Regression.png
|icon=Quantile Regression.svg
|simpleicon=Quantile Regression_Pure.svg
|developer=Dev.Team-DPS
|developer=Dev.Team-DPS
|productionstate=PC可用
|productionstate=PC可用
第19行： 第21行：
|nodeavailabletablelist=Table_For_Downstream
|nodeavailabletablelist=Table_For_Downstream
|nodeconfiguration=VariableList;Text
|nodeconfiguration=VariableList;Text
|nodeinputports=WorkFlow-Control ▶;Transfer-Table ■
|nodeinputports=WorkFlow-Control 🠶;Transfer-Variable ◆;Transfer-Table ■
|nodeoutputports=WorkFlow-Control ▶;Transfer-Table ■
|nodeoutputports=WorkFlow-Control 🠶;Transfer-Table ■
|statsapewikiurl=https://wiki.statsape.com/分位回归
|statsapewikiurl=https://wiki.statsape.com/分位回归
|previousnode=[[广义相加混合模型_逻辑]]
|previousnode=[[广义相加混合模型_逻辑]]
|nextnode=[[逐步回归]]
|nextnode=[[逐步回归]]
}}
}}




2023年12月8日 (五) 10:51的版本

Quantile Regression.png
节点状态
PC可用
在 V1.0部署
分位回归Quantile Regression.svg
节点开发者决策链算法研发部 (Dev.Team-DPS)
节点英文名分位回归
功能主类别数据分析
英文缩写QR
功能亚类别回归分析
节点类型数据挖掘
开发语言R
节点简介

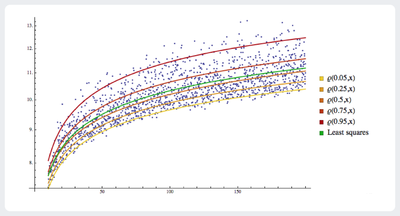
分位数回归是对一组自变量与因变量的特定百分位数(分位数)之间的关系建模。分位数回归的原因就是因为不希望仅仅是研究因变量y的期望，而是希望能探索y的完整分布状况，和了解y的某个分位数。优势是不会假设目标变量的分布,和趋向于抑制偏离观测值的影响。此算法用户可以输入设置任意分位数。

用途：关注因变量的均值如何随着自变量的变化而变化，而且还关注因变量的整个分布如何随着自变量的变化而变化。可以帮助研究这种非均匀的影响，自变量对因变量的影响可能随着因变量的值而变化。

参数：选择数值因变量，和自变量

端口数量与逻辑控制(PC)
Input-入口4个
Output-出口2个
Loop-支持循环是
If/Switch-支持逻辑判断否
输入输出
可生成图片类型（推荐）
可生成数据表类型（推荐）
相关节点
上一节点广义相加混合模型_逻辑
下一节点逐步回归
WikimediaUI-Globe.svg相关网站





查找其他类别的节点，请参考以下列表

取自“https://wiki.statsape.com/index.php?title=分位回归&oldid=3103”
最近修改
此页面最后编辑于2023年12月8日 (星期五) 10:51。
版权
DecisionLinnc Wiki (决策链云智库) © 2024 by Statsape is licensed under Attribution-NonCommercial-ShareAlike 4.0 International. To view a copy of this license, visit [http://creativecommons.org/licenses/by-nc-sa/4.0/| CreativeCommons-Licenses-4.0].