机器学习分类器系统

基于规则的机器学习方法范式
Zeroclanzhang（讨论 | 贡献）2024年1月23日 (二) 18:47的版本 （创建页面，内容为“{{Short description|基于规则的机器学习方法范式}} File:Function approximation with LCS rules.jpg|thumb|LCS规则学习近似3D函数的2D可视化效果图。每个蓝色椭圆代表覆盖解决方案空间一部分的单个规则。（改编自XCSF<ref name=":9">{{Cite journal|last1=Stalph|first1=Patrick O.|last2=Butz|first2=Martin V.|date=2010-02-01|title=JavaXCSF: The XCSF Learning Classifier System in Java|journal=SIGEVOlution|volume=4|issue=3…”）
(差异) ←上一版本 | 最后版本 (差异) | 下一版本→ (差异)
LCS规则学习近似3D函数的2D可视化效果图。每个蓝色椭圆代表覆盖解决方案空间一部分的单个规则。（改编自XCSF[1]的图像，并经Martin Butz授权）

学习分类系统（Learning classifier systems，缩写为LCS），是一种基于规则的机器学习方法范式，结合了发现组件（例如通常是遗传算法）和学习组件（执行监督学习、强化学习或无监督学习）[2]。学习分类系统旨在识别一组上下文相关的规则，这些规则集体存储并以分段方式应用知识以进行预测（例如行为建模[3]、分类[4][5]、数据挖掘[5][6][7]、回归[8]、函数逼近[9]或游戏策略）。这种方法允许将复杂的解决方案空间分解为更小、更简单的部分。

学习分类系统的创始概念源于试图模拟复杂适应系统，使用基于规则的代理形成人工认知系统（即人工智能）。

方法论

特定学习分类系统的架构和组件可能会有很大的变化。把LCS视为由几个相互作用的组件组成的机器是有帮助的。可以根据特定问题域的需求添加或移除组件，或修改/交换现有组件（如算法构建块），使算法足够灵活，可以在多个不同的问题域中发挥作用。因此，LCS范式可以灵活地应用于需要机器学习的许多问题域。LCS实现之间的主要区别如下：（1）Michigan风格架构与Pittsburgh风格架构之间的对比，[10]（2）强化学习与监督学习，（3）增量学习与批量学习，（4）在线学习与离线学习，（5）基于强度的适应度与基于准确性的适应度，以及（6）完整动作映射与最佳动作映射。这些区分并非相互排斥。例如，XCS，[11]最著名且研究最多的LCS算法，是Michigan风格的，设计用于强化学习但也可执行监督学习，应用增量学习可在线上或离线进行，应用基于准确性的适应度，并寻求生成完整动作映射。

通用LCS算法的要素

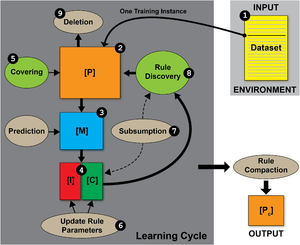
图解展示了一个通用的密歇根风格学习分类器系统在监督学习中的学习周期

考虑到LCS（学习分类器系统）是基于遗传的机器学习范式而不是特定方法，以下内容概述了通用、现代（即后XCS）LCS算法的关键要素。为了简化，我们专注于带有监督学习的密歇根风格架构。参见右侧的插图，展示了这类通用LCS所涉及的顺序步骤。

环境

环境是LCS学习的数据来源。它可以是一个离线的、有限的训练数据集（特征为数据挖掘、分类或回归问题），或在线的连续实时训练实例流。每个训练实例假定包含一定数量的特征（也称为属性，或独立变量），以及一个感兴趣的单一终点（也称为类别、动作、表型、预测或因变量）。LCS学习的一部分可能涉及特征选择，因此训练数据中的所有特征都不需要是信息性的。一个实例的特征值集合通常被称为状态。为了简化，假设一个示例问题域具有布尔/二进制特征和布尔/二进制类别。对于密歇根风格系统，每个学习周期中从环境中训练一个实例（即增量学习）。匹兹堡风格系统执行批量学习，在每次迭代中评估规则集，涵盖大部分或全部训练数据。

规则/分类器/种群

规则是状态值和某些预测之间的上下文依赖关系。规则通常采用{IF:THEN}表达形式（例如{IF '条件' THEN '动作'}, 或更具体的例子，{IF '红色' AND '八边形' THEN '停止标志'}）。LCS和基于规则的机器学习中的一个关键概念是，单个规则本身并不是一个模型，因为规则只有在其条件满足时才适用。可以将规则视为解决方案空间的“局部模型”。

规则可以以多种不同方式表示，以处理不同的数据类型（例如二进制、离散值、序数、连续值）。对于二进制数据，LCS传统上应用三元规则表示（即规则可以对数据中的每个特征包含0、1或'#'）。'不关心'符号（即'#'）在规则条件中充当通配符，允许规则和整个系统概括特征与目标终点之间的关系。考虑以下规则（#1###0 ~ 1）（即条件 ~ 动作）。这个规则可以解释为：如果第二个特征=1并且第六个特征=0，则类别预测=1。我们会说这条规则中指定了第二和第六个特征，而其他特征被泛化。这条规则及其相应的预测只有在实例满足规则条件时才适用。这通常被称为匹配。在密歇根风格LCS中，每个规则都有自己的适应度，以及与之相关的许多其他规则参数，可以描述该规则存在的副本数量（即数量），规则的年龄、其准确性或其奖励预测的准确性，以及其他描述性或经验性统计数据。规则及其参数通常被称为分类器。在密歇根风格系统中，分类器包含在用户定义的最大分类器数量的种群 [P] 中。与大多数随机搜索算法（例如进化算法）不同，LCS种群开始时是空的（即不需要随机初始化规则种群）。分类器将最初通过覆盖机制引入到种群中。

在任何LCS中，训练模型是一组规则/分类器，而不是任何单一规则/分类器。在密歇根风格LCS中，整个训练（以及可选的压缩）分类器种群形成了预测模型。

匹配

LCS中最关键且经常耗时的元素之一是匹配过程。LCS学习周期的第一步从环境中获取单个训练实例并传递给[P]，在此进行匹配。第二步中，[P]中的每条规则现在与训练实例进行比较，以查看哪些规则匹配（即与当前实例上下文相关）。第三步中，任何匹配的规则都被移动到匹配集 [M]。如果规则条件中指定的所有特征值与训练实例中相应的特征值相等，则该规则与训练实例匹配。例如，假设训练实例为（001001 ~ 0），则这些规则将匹配：（###0## ~ 0），（00###1 ~ 0），（#01001 ~ 1），但这些规则不会匹配（1##### ~ 0），（000##1 ~ 0），（#0#1#0 ~ 1）。注意，在匹配中，规则指定的终点/动作不予考虑。因此，匹配集可能包含提出相互冲突动作的分类器。在第四步中，由于我们进行的是监督学习，[M]被划分为正确集合[C]和错误集合[I]。如果匹配规则提出正确的动作（基于训练实例的已知动作），则进入正确集合；否则进入[I]。在强化学习LCS中，此时会形成一个动作集[A]，因为正确的动作是未知的。

覆盖（Covering）

在学习周期的这一点，如果没有分类器进入[M]或[C]（当种群开始为空时的情况），则应用覆盖机制（第五步）。覆盖是一种“在线智能种群初始化”的形式。覆盖随机生成一个与当前训练实例匹配的规则（在监督学习的情况下，该规则还生成正确的动作）。假设训练实例是（001001 ~ 0），覆盖可能生成以下任一规则：（#0#0## ~ 0）、（001001 ~ 0）、（#010## ~ 0）。覆盖不仅确保每个学习周期中[C]中至少有一个正确的匹配规则，而且确保初始化到种群中的任何规则至少与一个训练实例匹配。这可以防止LCS探索不匹配任何训练实例的规则的搜索空间。

参数更新/信用分配/学习（Parameter updates/credit assignment/learning）

在第六步，[M]中任何规则的参数都会更新，以反映从当前训练实例获得的新经验。根据LCS算法，可以在此步骤进行多种更新。对于监督学习，我们可以简单地更新规则的准确性/误差。规则准确性/误差与模型准确性/误差不同，因为它不是在整个训练数据上计算的，而是仅在所有匹配的实例上计算的。规则准确性是通过将规则在正确集[C]中的次数除以它在匹配集[M]中的次数来计算的。规则准确性可以被认为是一种“局部准确性”。规则适应性也在此处更新，通常作为规则准确性的函数来计算。适应性的概念直接来自经典的遗传算法。请注意，LCS在执行信用分配和学习时更新参数的方式有很多种变化。

次级吸收（Subsumption）

在第七步，通常会应用一种“次级吸收”机制。次级吸收是一个明确的概括机制，它合并覆盖问题空间冗余部分的分类器。次级吸收分类器有效地吸收被次级吸收的分类器（并增加其数量性）。这只会发生在次级吸收分类器更一般化、同样准确，并覆盖它所次级吸收的分类器的所有问题空间时。

规则发现/遗传算法（Rule discovery/genetic algorithm）

在第八步，LCS采用一种高度精英主义的遗传算法（GA），它将基于适应性（适者生存）选择两个父分类器。父分类器通常从[C]中使用锦标赛选择选出。有些系统应用了轮盘赌选择或确定性选择，并从[P] - 泛交配选择，或从[M]中不同地选择父规则。现在应用交叉和变异操作符来生成两个新的后代规则。此时，父规则和后代规则都被返回到[P]。LCS的遗传算法是高度精英主义的，因为每次学习迭代，绝大多数种群都被保留。规则发现也可以通过其他方法进行，例如分布估计算法，但GA是迄今为止最常用的方法。像GA这样的进化算法采用随机搜索，这使LCS成为一种随机算法。LCS旨在巧妙地探索搜索空间，但不执行规则组合的穷尽搜索，也无法保证收敛于最优解。

删除（Deletion）

在通用LCS学习周期的最后一步是维持最大种群大小。删除机制将选择分类器以进行删除（通常使用轮盘赌选择）。分类器被选为删除的概率与其适应性成反比。当选择了一个分类器进行删除时，其数量性参数会减少一个。当分类器的数量性减少到零时，它将完全从种群中移除。

训练（Training）

LCS将对这些步骤反复进行某个用户定义的训练迭代次数，或直到达到某个用户定义的终止标准。对于在线学习，LCS将在每次迭代中从环境中获得一个全新的训练实例。对于离线学习，LCS将遍历一个有限的训练数据集。一旦到达数据集中的最后一个实例，它将返回到第一个实例并再次遍历数据集。

规则压缩（Rule compaction）

一旦训练完成，规则种群将不可避免地包含一些质量差、冗余和缺乏经验的规则。通常会应用一种“规则压缩”或“凝聚”启发式作为后处理步骤。这种压缩后的规则种群准备好作为预测模型应用（例如，对测试实例进行预测），和/或用于知识发现。

预测

无论是否应用了规则压缩，学习分类系统（LCS）算法的输出是一组分类器，可用于对以前未见的实例进行预测。预测机制不是监督式LCS学习周期本身的一部分，但在强化学习LCS学习周期中扮演重要角色。目前，我们考虑如何将预测机制应用于对测试数据进行预测。在进行预测时，LCS学习组件被停用，以防止种群继续从进入的测试数据中学习。测试实例被传递给[P]，其中像往常一样形成匹配集[M]。此时，匹配集被不同地传递到预测数组中。匹配集中的规则可以预测不同的动作，因此应用了投票方案。在简单的投票方案中，从匹配规则中获得最强支持的“票数”的动作胜出，并成为选定的预测。并非所有规则都能平等投票。相反，单个规则的投票强度通常与其数量和适应性成比例。这种投票方案以及LCS存储知识的方式表明，LCS算法隐含地是“集成学习者”。

解释

LCS规则通常是人类可读的IF:THEN表达式。构成LCS预测模型的规则可以根据不同的规则参数进行排名并手动检查。也提出了使用统计和图形的全局策略来指导知识发现[12][13]。与其他先进的机器学习方法（如人工神经网络、随机森林或遗传编程）相比，学习分类系统特别适合于需要可解释解决方案的问题。

历史

早期

John Henry Holland因其推广遗传算法（GA）的工作而闻名，尤其是通过其1975年的开创性著作《自然和人工系统中的适应》[14]以及他对荷兰模式定理的正式阐述。1976年，Holland构想了GA概念的一个扩展，称之为“认知系统”，[15]并提供了将成为第一个学习分类系统的详细描述，论文名为“基于自适应算法的认知系统”。[16] 这个最初的系统，名为Cognitive System One (CS-1)，被构想为一种建模工具，旨在使用一组人类可读规则来模拟具有未知底层动态的真实系统（即环境）。该规则集的目标是执行在线机器学习，根据不频繁的支付/奖励（即强化学习）适应环境，并应用这些规则生成与真实系统相匹配的行为。这种早期、雄心勃勃的实现后来被认为过于复杂，产生不一致的结果。[2][17]

自1980年起，Kenneth de Jong及其学生Stephen Smith采取了不同的基于规则的机器学习方法，即(LS-1)，在此方法中，学习被视为一种离线优化过程，而不是在线适应过程。[18][19][20] 这种新方法更类似于标准的遗传算法，但进化了独立的规则集。自那时起，受Holland在密歇根大学引入的在线学习框架启发的LCS方法被称为密歇根式LCS，而受Smith和De Jong在匹兹堡大学启发的方法被称为匹兹堡式LCS。[2][17] 1986年，Holland开发了下一个十年被视为标准的密歇根式LCS。[21]

在学习分类器系统（LCS）研究的早期，出现了一些重要的概念，包括：

1. 为信用分配/学习而形式化的“桶接力算法”（BBA）[22]； 2. 从共同的“环境生态位”（即“匹配集合”[M]）而非整个“种群”[P]中选择父规则[23]； 3. 首次作为“创建”操作引入的“覆盖”[24]； 4. “动作集合”[A]的形式化[24]； 5. 算法架构的简化[24]； 6. “基于强度的适应度”[21]； 7. 考虑单步骤或监督学习问题及“正确集合”[C]的引入[25]； 8. “基于准确度的适应度”[26]； 9. 将模糊逻辑与LCS结合[27]（后来衍生出一系列“模糊LCS算法”）； 10. 为提高多步问题的性能，鼓励“长动作链”和“默认层级”[28][29][30]； 11. 研究潜在学习（后来启发了新分支“预期分类器系统”(ACS)）[31]； 12. 引入了首个类Q学习的信用分配技术[32]。

虽然并非所有这些概念都应用于现代LCS算法中，但每一个都是LCS范式发展的里程碑。

革命

20世纪90年代中期，由于两个事件，对学习分类器系统的兴趣重新焕发活力：一是Q-学习算法的发展[33]，二是Stewart Wilson引入的显著简化的密歇根风格LCS架构[11][34]。Wilson的零级分类器系统（ZCS）[34]致力于基于Holland标准LCS实现的算法可理解性的提升[21]。这部分是通过移除原始BBA信用分配中至关重要的规则竞价和内部消息列表，并用混合BBA/Q-Learning策略替代之来实现的。ZCS证明了，一个更简单的LCS架构可以像原来更复杂的实现一样表现良好。然而，ZCS仍然存在性能上的缺陷，包括过于泛化的分类器的增多。

在1995年，威尔逊发表了其里程碑式的论文《基于准确度的分类器适应性》，他在其中介绍了分类器系统XCS。[11] XCS采用了ZCS的简化架构，并增加了基于准确度的适应性、一个在行动集[A]中起作用的利基遗传算法（niche GA）、一个名为覆盖的显式泛化机制，以及对Q-学习信用分配的改进。XCS因其在进化精确且尽可能泛化的分类器时达到最优性能，以及其令人印象深刻的问题灵活性（能够执行强化学习和监督学习）而受到推崇。XCS后来成为最著名、研究最多的LCS算法，并定义了一个新的基于准确性的LCS族。相反，ZCS则成为基于强度的LCS的代名词。XCS还因为成功地弥合了LCS与强化学习领域之间的差距而具有重要意义。在XCS成功之后，LCS后来被描述为具有泛化能力的强化学习系统。[35] 强化学习通常旨在学习一个价值函数，该函数映射出状态/动作空间的完整表示。同样，XCS的设计使其形成对问题空间的全面且准确的表示（即完整地图），而不是专注于环境中的高回报利基（如基于强度的LCS所做的）。从概念上讲，完整地图不仅捕捉你应该做什么、或者什么是正确的，还捕捉你不应该做什么、或者什么是错误的。不同地，大多数基于强度的LCS，或专门的监督学习LCS寻求一套高效泛化规则，形式为最佳行动地图（或部分地图）。自那时以来，基于强度与基于准确度的适应性以及完整地图与最佳行动地图之间的比较已被更详细地研究。[36][37]

XCS的影响

XCS激发了一整代新的LCS算法和应用的发展。1995年，康登首次将LCS应用于现实世界中的流行病学疾病调查[38]，紧接着霍尔姆斯开发了BOOLE++，[39] EpiCS，[40]以及后来的EpiXCS[41]，用于流行病学分类。这些早期工作激发了后来在复杂和大规模数据挖掘任务中应用LCS算法的兴趣，尤其是生物信息学应用。1998年，斯托尔兹曼引入了预期分类器系统（ACS），其中包括了形式为'条件-动作-效果'的规则，而非经典的'条件-动作'表示。[31] ACS旨在预测一个动作在所有可能的环境情境中的感知后果。换句话说，该系统进化出一个模型，不仅指定在给定情境中要做什么，还提供特定动作执行后会发生什么的信息。这类LCS算法最适合多步问题、规划、加速学习，或消除感知别名（即，在不同状态获得相同观察但需要不同动作的情况）。之后，布茨继续发展这一预期LCS家族，对原始方法进行了若干改进。[42] 2002年，威尔逊引入了XCSF，增加了计算动作以进行函数逼近。[43] 2003年，伯纳多-曼西拉引入了监督分类器系统（UCS），该系统专门化了XCS算法，用于监督学习、单步问题，并形成最佳行动集。UCS去除了强化学习策略，转而采用简单的基于准确度的规则适应性以及许多强化学习者特有的探索/利用学习阶段。布尔引入了一个简单的基于准确度的LCS(YCS)[44] 以及一个基于简单强度的LCS系统 最小分类器系统（MCS）[45]，以便更好地理解LCS框架的理论基础。Bacardit介绍了GAssist[46] 和 BioHEL,[47] 这些为数据挖掘和在生物信息学应用中的大型数据集可扩展性而设计的匹兹堡风格LCS系统。2008年，Drugowitsch出版了名为“学习分类器系统的设计与分析”的书籍，其中包括对LCS算法的一些理论考量。[48] Butz首次在XCSF的GUI中引入了在线规则学习的可视化。[1] (见本页顶部的图片)。Urbanowicz扩展了UCS框架，并引入了ExSTraCS, 显式设计用于噪声问题领域（例如流行病学和生物信息学）的监督学习。[49] ExSTraCS整合了(1) 利用专家知识引导覆盖和遗传算法指向数据中的重要特征,[50] (2) 一种称为属性跟踪的长期记忆形式,[51] 使得学习更高效，且能够描述异质数据模式，以及 (3) 类似于Bacardit混合离散-连续属性列表表示的灵活规则表示。[52] Bacardit和Urbanowicz探索了统计和可视化策略，以解释LCS规则并进行数据挖掘的知识发现。[12][13] Browne和Iqbal探索了以代码片段形式重用构建块的概念，并且是首次通过首先从简单的多路复用器问题中学习有用的构建块来解决135位多路复用器基准问题。[53] ExSTraCS 2.0 被后续引入以提高密歇根风格学习分类系统（LCS）的可扩展性，首次直接成功解决了135位多路复用器基准问题。[5] n位多路复用器问题具有高度的表型互作和同质与异质性，使其成为一个极具挑战性的机器学习任务。

变种

密歇根风格学习分类系统

密歇根风格的LCS以规则群体为特征，其中遗传算法在个体规则层面上操作，解决方案由整个规则群体表示。密歇根风格系统还可以进行增量学习，允许它们同时进行强化学习和监督学习，以及在线和离线学习。密歇根风格系统的优势在于适用于更多问题领域，以及增量学习的独特好处。

匹兹堡风格学习分类系统

匹兹堡风格的LCS以变长规则集的群体为特征，其中每个规则集都是潜在的解决方案。遗传算法通常在整个规则集的层面上操作。匹兹堡风格系统还可以独特地进化有序规则列表，以及使用默认规则。这些系统自然具有识别较小规则集的优势，使得这些系统在手动规则检查方面更具解释性。

混合系统

也有人提出了结合这两种系统关键优势的系统。

优点

  • 自适应：它们可以适应在线学习中的变化环境。
  • 无模型：它们对环境或数据中的关联模式的假设有限。
    • 它们可以在不依赖先验知识的情况下模拟复杂的、表型互作的、异质的或分布式的潜在模式。
    • 它们对数据中预测特征与非预测特征的数量不做假设。
  • 集成学习者：没有单一模型被普遍应用于给定实例以提供预测。相反，一组相关且常常相互冲突的规则贡献了一个“投票”，可以被解释为模糊预测。
  • 随机学习者：非确定性学习在大规模或高复杂性问题中有优势，在这些问题中，确定性或穷尽式学习变得难以实现。
  • 隐含的多目标性：规则朝着准确性演化，隐含和明确的压力鼓励最大的普遍性/简单性。这种隐含的泛化压力是LCS独有的。实际上，更普遍的规则会更频繁地出现在匹配集中。反过来，它们有更频繁的机会被选为父本，并将它们更普遍的（基因组）传递给后代规则。
  • 可解释性：出于数据挖掘和知识发现的兴趣，个别LCS规则是逻辑的，并且可以被制成人类可解释的IF:THEN语句。还引入了有效的策略，以便进行全局知识发现，识别整个规则群体中的重要特征和关联模式。[12]
  • 灵活应用
    • 单步或多步问题
    • 监督学习、强化学习或无监督学习
    • 二元类别和多类别分类
    • 回归
    • 离散或连续特征（或两种类型的混合）
    • 干净或噪声问题领域
    • 平衡或不平衡的数据集。
    • 适应缺失数据（即训练实例中缺失的特征值）

缺点

  • 软件可用性有限：开源、易于访问的LCS实现数量有限，且设计为对机器学习从业者友好或易于使用的更少。
  • 解释性：虽然LCS算法比某些高级机器学习者更具可解释性，但用户必须解释一组规则（有时是大量规则集以理解LCS模型）。规则压缩和解释策略的方法仍是一个活跃的研究领域。
  • 理论/收敛证明：LCS算法背后的理论工作相对较少。这可能是由于它们相对的算法复杂性（应用多个相互作用的组件）以及它们的随机性。
  • 过拟合：像任何机器学习者一样，尽管有隐含和明确的泛化压力，LCS也可能遭受过拟合。
  • 运行参数：LCS通常有许多需要考虑/优化的运行参数。通常，大多数参数可以保留为社区确定的默认值，但有两个关键参数例外：最大规则群体大小和最大学习迭代次数。优化这些参数可能非常依赖于问题。
  • 知名度：尽管LCS算法已经存在多年，但在机器学习社区中仍不为人所知。因此，LCS算法在与其他成熟的机器学习方法相比时很少被考虑。这可能是由于以下因素：（1）LCS是一种相对复杂的算法方法，（2）LCS的基于规则的建模是与几乎所有其他机器学习方法不同的建模范式。（3）LCS软件实现不常见。
  • 计算成本高：虽然比某些穷尽的方法更可行，但LCS算法可能计算成本高。对于简单的线性学习问题，没有必要应用LCS。LCS算法最适合于复杂的问题空间，或者几乎没有先验知识的问题空间。

问题领域

  • 自适应控制
  • 数据挖掘
  • 工程设计
  • 特征选择
  • 函数逼近
  • 游戏玩法
  • 图像分类
  • 知识处理
  • 医学诊断
  • 建模
  • 导航
  • 优化
  • 预测
  • 查询
  • 机器人技术
  • 路由
  • 规则归纳
  • 调度
  • 策略

术语

“学习分类器系统（LCS）”这个名字有些误导性，因为许多机器学习算法都具有'学习分类'的能力（例如决策树、人工神经网络），但它们并不是LCS。'基于规则的机器学习（RBML）'这个术语很有用，因为它更清楚地捕捉到这些系统的'基于规则'的核心组成部分，但它也泛化到不被视为LCS的方法（例如关联规则学习或人工免疫系统）。更通用的术语，如'基于遗传的机器学习'，甚至是'遗传算法'[38]也被用来指代更典型地定义为学习分类器系统的内容。由于它们与遗传算法的相似性，匹兹堡风格的学习分类器系统有时泛称为'遗传算法'。除此之外，一些LCS算法或与之密切相关的方法被称为'认知系统',[16] '自适应代理'，'生产系统'，或一般性地称为'分类器系统'。[54][55] 这种术语的多样性导致了该领域的一些混淆。

直到2000年代，几乎所有的学习分类器系统方法都是以强化学习问题为目标开发的。因此，'学习分类器系统'这一术语通常被定义为'试错'强化学习与遗传算法的全局搜索的结合。对监督学习应用的兴趣，甚至是非监督学习的兴趣，自此扩展了这一术语的使用和定义。

另行参见

引用

  1. ↑ 1.0 1.1 Stalph, Patrick O.; Butz, Martin V. (2010-02-01). "JavaXCSF: The XCSF Learning Classifier System in Java". SIGEVOlution. 4 (3): 16–19. doi:10.1145/1731888.1731890. ISSN 1931-8499. S2CID 16861908.
  2. ↑ 2.0 2.1 2.2 Urbanowicz, Ryan J.; Moore, Jason H. (2009-09-22). "Learning Classifier Systems: A Complete Introduction, Review, and Roadmap". Journal of Artificial Evolution and Applications (in English). 2009: 1–25. doi:10.1155/2009/736398. ISSN 1687-6229.
  3. ↑ Dorigo, Marco (1995). "Alecsys and the AutonoMouse: Learning to control a real robot by distributed classifier systems". Machine Learning (in English). 19 (3): 209–240. doi:10.1007/BF00996270. ISSN 0885-6125.
  4. ↑ Bernadó-Mansilla, Ester; Garrell-Guiu, Josep M. (2003-09-01). "Accuracy-Based Learning Classifier Systems: Models, Analysis and Applications to Classification Tasks". Evolutionary Computation. 11 (3): 209–238. doi:10.1162/106365603322365289. ISSN 1063-6560. PMID 14558911. S2CID 9086149.
  5. ↑ 5.0 5.1 5.2 Urbanowicz, Ryan J.; Moore, Jason H. (2015-04-03). "ExSTraCS 2.0: description and evaluation of a scalable learning classifier system". Evolutionary Intelligence (in English). 8 (2–3): 89–116. doi:10.1007/s12065-015-0128-8. ISSN 1864-5909. PMC 4583133. PMID 26417393.
  6. ↑ Bernadó, Ester; Llorà, Xavier; Garrell, Josep M. (2001-07-07). "XCS and GALE: A Comparative Study of Two Learning Classifier Systems on Data Mining". In Lanzi, Pier Luca; Stolzmann, Wolfgang; Wilson, Stewart W. (eds.). Advances in Learning Classifier Systems. Lecture Notes in Computer Science (in English). Vol. 2321. Springer Berlin Heidelberg. pp. 115–132. doi:10.1007/3-540-48104-4_8. ISBN 9783540437932.
  7. ↑ Bacardit, Jaume; Butz, Martin V. (2007-01-01). "Data Mining in Learning Classifier Systems: Comparing XCS with GAssist". In Kovacs, Tim; Llorà, Xavier; Takadama, Keiki; Lanzi, Pier Luca; Stolzmann, Wolfgang; Wilson, Stewart W. (eds.). Learning Classifier Systems. Lecture Notes in Computer Science (in English). Vol. 4399. Springer Berlin Heidelberg. pp. 282–290. CiteSeerX 10.1.1.553.4679. doi:10.1007/978-3-540-71231-2_19. ISBN 9783540712305.
  8. ↑ Urbanowicz, Ryan; Ramanand, Niranjan; Moore, Jason (2015-01-01). "Continuous Endpoint Data Mining with ExSTraCS". Proceedings of the Companion Publication of the 2015 Annual Conference on Genetic and Evolutionary Computation. GECCO Companion '15. New York, NY, USA: ACM. pp. 1029–1036. doi:10.1145/2739482.2768453. ISBN 9781450334884. S2CID 11908241.
  9. ↑ Butz, M. V.; Lanzi, P. L.; Wilson, S. W. (2008-06-01). "Function Approximation With XCS: Hyperellipsoidal Conditions, Recursive Least Squares, and Compaction". IEEE Transactions on Evolutionary Computation. 12 (3): 355–376. doi:10.1109/TEVC.2007.903551. ISSN 1089-778X. S2CID 8861046.
  10. ↑ [引入基于规则的机器学习：实用指南]，Ryan J. Urbanowicz和Will Browne，见72-73页的Michigan风格架构与Pittsburgh风格架构的比较。
  11. ↑ 11.0 11.1 11.2 Wilson, Stewart W. (1995-06-01). "Classifier Fitness Based on Accuracy". Evol. Comput. 3 (2): 149–175. CiteSeerX 10.1.1.363.2210. doi:10.1162/evco.1995.3.2.149. ISSN 1063-6560. S2CID 18341635.
  12. ↑ 12.0 12.1 12.2 Urbanowicz, R. J.; Granizo-Mackenzie, A.; Moore, J. H. (2012-11-01). "密歇根风格学习分类器系统的统计和可视化引导知识发现分析管道". IEEE 计算智能杂志. 7 (4): 35–45. doi:10.1109/MCI.2012.2215124. ISSN 1556-603X. PMC 4244006. PMID 25431544.
  13. ↑ 13.0 13.1 Bacardit, Jaume; Llorà, Xavier (2013). "使用基于遗传的机器学习进行大规模数据挖掘". Wiley 综合评论: 数据挖掘与知识发现. 3 (1): 37–61. doi:10.1002/widm.1078. S2CID 43062613.
  14. ↑ Holland, John (1975). Adaptation in natural and artificial systems: an introductory analysis with applications to biology, control, and artificial intelligence. Michigan Press. ISBN 9780262581110.
  15. ↑ Holland JH (1976) Adaptation. In: Rosen R, Snell F (eds) Progress in theoretical biology, vol 4. Academic Press, New York, pp 263–293
  16. ↑ 16.0 16.1 Holland JH, Reitman JS (1978) Cognitive systems based on adaptive algorithms Reprinted in: Evolutionary computation. The fossil record. In: David BF (ed) IEEE Press, New York 1998. ISBN 0-7803-3481-7
  17. ↑ 17.0 17.1 Lanzi, Pier Luca (2008-02-08). "Learning classifier systems: then and now". Evolutionary Intelligence (in English). 1 (1): 63–82. doi:10.1007/s12065-007-0003-3. ISSN 1864-5909. S2CID 27153843.
  18. ↑ Smith S (1980) A learning system based on genetic adaptive algorithms. Ph.D. thesis, Department of Computer Science, University of Pittsburgh
  19. ↑ Smith S (1983) Flexible learning of problem solving heuristics through adaptive search. In: Eighth international joint conference on articial intelligence. Morgan Kaufmann, Los Altos, pp 421–425
  20. ↑ De Jong KA (1988) Learning with genetic algorithms: an overview. Mach Learn 3:121–138
  21. ↑ 21.0 21.1 21.2 Holland, John H. "Escaping brittleness: the possibilities of general purpose learning algorithms applied to parallel rule-based system." Machine learning(1986): 593-623.
  22. ↑ Holland, John H. (1985-01-01). Properties of the Bucket Brigade. Hillsdale, NJ, USA: L. Erlbaum Associates Inc. pp. 1–7. ISBN 978-0805804263. {{cite book}}: |journal= ignored (help)
  23. ↑ Booker, L (1982-01-01). Intelligent Behavior as an Adaptation to the Task Environment (Thesis). University of Michigan.
  24. ↑ 24.0 24.1 24.2 Wilson, S. W. "Knowledge growth in an artificial animal. Proceedings of the First International Conference on Genetic Algorithms and their Applications." (1985).
  25. ↑ Wilson, Stewart W. (1987). "Classifier systems and the animat problem". Machine Learning (in English). 2 (3): 199–228. doi:10.1007/BF00058679. ISSN 0885-6125.
  26. ↑ Frey, Peter W.; Slate, David J. (1991). "Letter recognition using Holland-style adaptive classifiers". Machine Learning (in English). 6 (2): 161–182. doi:10.1007/BF00114162. ISSN 0885-6125.
  27. ↑ Valenzuela-Rendón, Manuel. "The Fuzzy Classifier System: A Classifier System for Continuously Varying Variables." In ICGA, pp. 346-353. 1991.
  28. ↑ Riolo, Rick L. (1988-01-01). Empirical Studies of Default Hierarchies and Sequences of Rules in Learning Classifier Systems (Thesis). Ann Arbor, MI, USA: University of Michigan.
  29. ↑ R.L., Riolo (1987-01-01). "Bucket brigade performance. I. Long sequences of classifiers". Genetic Algorithms and Their Applications: Proceedings of the Second International Conference on Genetic Algorithms: July 28–31, 1987 at the Massachusetts Institute of Technology, Cambridge, MA (in English).
  30. ↑ R.L., Riolo (1987-01-01). "Bucket brigade performance. II. Default hierarchies". Genetic Algorithms and Their Applications: Proceedings of the Second International Conference on Genetic Algorithms: July 28–31, 1987 at the Massachusetts Institute of Technology, Cambridge, MA (in English).
  31. ↑ 31.0 31.1 W. Stolzmann, "Anticipatory classifier systems," in Proceedings of the 3rd Annual Genetic Programming Conference, pp. 658–664, 1998.
  32. ↑ Riolo, Rick L. (1990-01-01). Lookahead Planning and Latent Learning in a Classifier System. Cambridge, MA, USA: MIT Press. pp. 316–326. ISBN 978-0262631389. {{cite book}}: |journal= ignored (help)
  33. ↑ Watkins, Christopher John Cornish Hellaby. "Learning from delayed rewards." PhD diss., University of Cambridge, 1989.
  34. ↑ 34.0 34.1 Wilson, Stewart W. (1994-03-01). "ZCS: A Zeroth Level Classifier System". Evolutionary Computation. 2 (1): 1–18. CiteSeerX 10.1.1.363.798. doi:10.1162/evco.1994.2.1.1. ISSN 1063-6560. S2CID 17680778.
  35. ↑ Lanzi, P. L. (2002). "从强化学习的视角学习分类器系统". Soft Computing (in English). 6 (3–4): 162–170. doi:10.1007/s005000100113. ISSN 1432-7643. S2CID 39103390.
  36. ↑ Kovacs, Timothy Michael Douglas. 比较学习与分类系统中基于强度和准确度的适应性。2002。
  37. ↑ Kovacs, Tim. "分类器系统的两种观点." 在国际学习分类器系统研讨会中，第74-87页。Springer Berlin Heidelberg, 2001
  38. ↑ 38.0 38.1 Congdon, Clare Bates. "A comparison of genetic algorithms and other machine learning systems on a complex classification task from common disease research." 博士论文，密歇根大学，1995年。
  39. ↑ Holmes, John H. (1996-01-01). "基于遗传的机器学习方法在临床数据中的知识发现". AMIA年度秋季研讨会论文集: 883. ISSN 1091-8280. PMC 2233061.
  40. ↑ Holmes, John H. "[ 使用学习分类器系统发现疾病风险]." 在ICGA中，第426-433页。1997。
  41. ↑ Holmes, John H., and Jennifer A. Sager. "使用EpiXCS在流行病学监测数据中发现规则：一种进化计算方法." 在欧洲人工智能医学会议中，第444-452页。Springer Berlin Heidelberg, 2005。
  42. ↑ Butz, Martin V. "[ 在预期学习分类器系统中偏向探索]." 在国际学习分类器系统研讨会中，第3-22页。Springer Berlin Heidelberg, 2001。
  43. ↑ Wilson, Stewart W. (2002). "近似函数的分类器". Natural Computing (in English). 1 (2–3): 211–234. doi:10.1023/A:1016535925043. ISSN 1567-7818. S2CID 23032802.
  44. ↑ Bull, Larry. "[ 一个简单的基于准确度的学习分类器系统]." “西英格兰大学布里斯托尔分校学习分类器系统小组技术报告UWELCSG03-005”（2003年）。
  45. ↑ Bull, Larry. "一个基于简单回报的学习分类器系统." 在国际自然并行问题解决大会中, 页 1032-1041. Springer Berlin Heidelberg, 2004.
  46. ↑ Peñarroya, Jaume Bacardit. "匹兹堡基因机器学习在数据挖掘时代：表示、概括与运行时间." 博士论文, Universitat Ramon Llull, 2004.
  47. ↑ Bacardit, Jaume; Burke, Edmund K.; Krasnogor, Natalio (2008-12-12). "提高基于规则的进化学习的可扩展性". Memetic Computing (in English). 1 (1): 55–67. doi:10.1007/s12293-008-0005-4. ISSN 1865-9284. S2CID 775199.
  48. ↑ Drugowitsch, Jan (2008). 学习分类器系统的设计与分析 - Springer. Studies in Computational Intelligence. Vol. 139. doi:10.1007/978-3-540-79866-8. ISBN 978-3-540-79865-1.
  49. ↑ Urbanowicz, Ryan J., Gediminas Bertasius, 和 Jason H. Moore. "用于灵活的监督学习、分类和数据挖掘的扩展密歇根风格学习分类器系统." 在国际自然并行问题解决大会中, 页 211-221. Springer International Publishing, 2014.
  50. ↑ Urbanowicz, Ryan J., Delaney Granizo-Mackenzie, 和 Jason H. Moore. "[ 使用专家知识引导覆盖和突变，在密歇根风格学习分类器系统中检测上位性和异质性]." 在国际自然并行问题解决大会中, 页 266-275. Springer Berlin Heidelberg, 2012.
  51. ↑ Urbanowicz, Ryan; Granizo-Mackenzie, Ambrose; Moore, Jason (2012-01-01). "与实例链接的属性跟踪和反馈，用于密歇根风格监督学习分类器系统". 遗传与进化计算年会论文集的第14届会议. GECCO '12. New York, NY, USA: ACM. pp. 927–934. doi:10.1145/2330163.2330291. ISBN 9781450311779. S2CID 142534.
  52. ↑ Bacardit, Jaume; Krasnogor, Natalio (2009-01-01). "用于大规模分类领域的混合离散-连续属性列表表示". 遗传与进化计算年会论文集的第11届会议. GECCO '09. New York, NY, USA: ACM. pp. 1155–1162. CiteSeerX 10.1.1.158.7314. doi:10.1145/1569901.1570057. ISBN 9781605583259. S2CID 10906515.
  53. ↑ Iqbal, Muhammad; Browne, Will N.; Zhang, Mengjie (2014-08-01). "重用提取知识的构建块来解决复杂的大规模布尔问题". IEEE Transactions on Evolutionary Computation. 18 (4): 465–480. doi:10.1109/tevc.2013.2281537. S2CID 525358.
  54. ↑ Booker, L. B.; Goldberg, D. E.; Holland, J. H. (1989-09-01). "分类器系统和遗传算法" (PDF). 人工智能. 40 (1): 235–282. doi:10.1016/0004-3702(89)90050-7. hdl:2027.42/27777.
  55. ↑ Wilson, Stewart W., and David E. Goldberg. "对分类器系统的关键评述." 在 遗传算法第三届国际会议论文集，第244-255页。Morgan Kaufmann出版社，1989年。

外部链接

世界维基百科视频教程

相关网站

取自“https://wiki.statsape.com/index.php?title=机器学习分类器系统&oldid=8489”