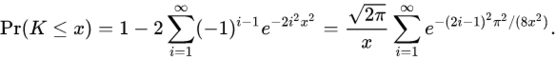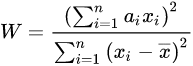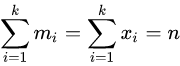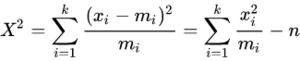正态性检验用于检查某观测值是否符合正态分布。检验正态分布的方法是将样本数据的直方图与标准正态曲线进行比较，或者将样本数据的标准化后的分位数与正态分布的标准分位数比较，简称Q-Q图。在Q-Q图中，样本数据和正态数据的相关性可以反映数据是否符合正态分布，对于正态数据，在Q-Q图中的散点近似于一条直线，表明高度正相关。此时也很容易观察到异常值。
本模块用于单变量正态性检验，检验方法有 Anderson–Darling， Cramér–von-Mise， Lilliefors（Kolmogorov-Smirnov），Chi-Squared Test和Shapiro–Francia检验。Cramér–von-Mises检验可用于小样本（n≤25）， 对于样本量 ≥200 可以采用 Anderson–Darling检验。
一、柯尔莫哥洛夫-斯米尔诺夫检验（Kolmogorov-Smirnov test，简称K-S test），是一种基于累计分布函数的非参数检验，用以检验两个经验分布是否不同或一个经验分布与另一个理想分布是否不同。本检验以安德雷·柯尔莫哥洛夫（Kolmogorov，俄语：Колмогоров）和尼古拉·斯米尔诺夫（Smirnov，俄语：Смирнов）之名作命名。
柯尔莫哥洛夫分布（kolmogorov distribution）是随机变量
的分布，其中 是布朗桥。K的累积分布函数由下式给出
柯尔莫哥洛夫-斯米尔诺夫检验的统计量形式及其在零假设下的渐近分布是由安德雷·柯尔莫哥洛夫提出的。
二、夏皮罗一威尔克检验法（Shapiro-Wilk），检验样本容量8≤n ≤50时，样本是否符合正态分布的一种方法。（现研究已实现样本扩大，n<5000，可应用于大部分正态分布）
其检验步骤如下：
①将数据按数值大小重新排列，使x1≤x2≤…≤xn；
②计算上式分母；
③计算a值，可查表得出；
④计算检验统计量W；
⑤若W值小于判断界限值Wα（可通过查表求得），按表上行写明的显著性水平α舍弃正态性假设；若W>Wα,接受正态性假设。
三、卡方检验（Chi-Squared Test）
是一种统计量的分布在零假设成立时近似服从卡方分布（分布）的假设检验。在没有其他的限定条件或说明时，卡方检验一般代指的是皮尔森卡方检定。在卡方检验的一般运用中，研究人员将观察量的值划分成若干互斥的分类，并且使用一套理论（或零假设）尝试去说明观察量的值落入不同分类的概率分布的模型。而卡方检验的目的就在于去衡量这个假设对观察结果所反映的程度。
假设实验中从总体中随机取样得到的个观察值被划分为个互斥的分类，这样每个分类都有一个对应的实际观察次数
（
）。研究人员会对实验中各个观察值落入第个
分类的概率
的分布提出零假设，从而获得了对应所有第分类的理论期望次数
以及限制条件
以及 
。
皮尔森提出，在上述零假设成立
以及趋向
的时候，以下统计量的极限分布趋向
分布。
皮尔森首先讨论零假设中所有分类的理论期望次数
均为足够大且已知的情况，同时假设各分类的实际观测次数均服从正态分布。皮尔森由此得到当样本容量足够大时，趋近服从自由度
为的分布。