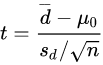两独立样本均数比较 t 检验用于比较两样本所分别代表的总体均数是否有统计学差异。理论上，即使样本量很小时，也可以进行 t 检验,如样本量为10。一些学者声称甚至更小的样本也行，只要每组中变量呈正态分布，两组方差不是明显不同。正态分布假设可以通过观察数据的分布（如直方图、箱体图、Q-Q图）或进行正态性检验来测量。方差齐性的假设可进行F检验，或进行更有效的 Levene's 检验。如果不满足这些条件，使用非参数检验代替 t 检验进行两组间均值的比较。如果呈正态分布，但方差不齐，可采用 Welch's t test 方法。
一、双侧检验还是单侧检验
t 检验中的P值是指拒绝无效假设的犯错概率。一些学者认为如果差异具有特定的方向性，就可只考虑单侧概率分布，将所得到t-检验的P值分为两半。另一些学者则认为无论何种情况下都要报告标准的双侧 t 检验概率。
二、配对数据
对于配对数据，采用配对 t 检验。配对 t 检验的基本原理是计算每对的差值（X=X1-X2），然后采用单样本T检验方法，检验差值是否等于0，以此推断配对样本间是否有显著差异。首先计算每对两数据之间的差，然后比较这些差值与0之间存在差异的概率。
三、数据结构
非配对数据：须有一个两分类的分组变量，指明对其所代表的两组进行比较。如分组变量为性别 SEX（1=男，2=女），表明对男与女之间进行比较。
配对数据：有横向数据与纵向数据两种。
横向数据：一条记录代表一对，用两个变量如（X1、X2）代表一对观测值。给定两个变量名，软件分别采用配对和非配对两个 t检验方法比较两个变量。此时不能指定分组变量，否则软件自动按非配对数据，对两个变量分别做两组间的比较。
纵向数据：每对观测单位有两条记录，有一个共同的配对组号，表示它们属于同一对。此时需要先对数据进行处理，采用【数据操作】-【数据结构重组】-【纵向数据转换成横向数据】模块，将每对的两条记录转化为1条记录，原先代表某观测指标的一个变量转化为2个变量（如X1，X2）。
四、配对t检验
配对样本t检验可视为单样本t检验的扩展，不过检验的对象由一群来自正态分配独立样本更改为两配对样本之观测值之差。
若两配对样本x1i与x2i之差为di = x1i − x2i独立且来自正态分配，则di之总体期望值μ是否为μ0可利用以下统计量：
其中，
，
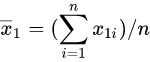及 
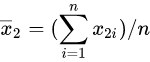为两样本各自的平均数，
，为样本之共同方差。该统计量t在零假设：μ1 - μ2 = μ0为真的条件下服从自由度为2n − 2的t分布。